裏 RjpWiki

算額（その873）

会田安明：算法天生法指南，文化7年(1810)
京都大学貴重資料デジタルアーカイブ
https://rmda.kulib.kyoto-u.ac.jp/item/rb00028519#?c=0&m=0&s=0&cv=95&r=0&xywh=-487%2C-149%2C4481%2C2977

横長の紙をおみくじ上に結ぶ。紙の幅が一寸のとき正五角形の一辺の長さはいかほどか。

正五角形の一辺の長さ(ab)を x，紙の幅(ac)を y とする。
図において，∠bac = 18° である。
x*cosd(18) = y より，y が与えられたとき x = 2√2y/sqrt(√5 + 5)を求める。

include("julia-source.txt");

using SymPy
@syms x, y
eq = x*cosd(Sym(18)) - y
x = solve(eq, x)[1]
x |> println

   2*sqrt(2)*y/sqrt(sqrt(5) + 5)

紙の幅が 1 寸のとき，正五角形の一辺の長さは 1.0514622242382672 寸である。

x(y => 1).evalf() |> N

   1.0514622242382672

算額（その872）

大阪府茨木市 井於神社 弘化3年(1846)
http://www.wasan.jp/osaka/iyo.html

大球の中に，小球 3 個と，中球 1 個が入っている。大球と小球の直径がそれぞれ 1 尺 2 寸と 4 寸 8 分のとき，中球の直径を求めよ。

eq1, eq2: y 軸の負の無限大方向から x-z 平面を見ると，小球は大球に内接し，中級と外接している。

eq3: 3 次元空間，x-y-z 軸で考える。z 軸の正の無限大方向から x-y 平面を見ると，小球 3 個は互いに接しており，その中心を結ぶと正三角形になる。

大球の半径と中心座標を r1, (0, 0, 0)
中球の半径と中心座標を r2, (0, 0, r1 - r2)
小球の半径と中心座標を r3, (x3, 0, z3); z3 < 0
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms r1::positive, r2::positive, r3::positive, x3::positive, z3::negative
(r1, r3) = (120, 48) .// 20
eq1 = x3^2 + z3^2 - (r1 - r3)^2
eq2 = x3^2 + (r1 - r2 - z3)^2 - (r2 + r3)^2
eq3 = x3√Sym(3)/2 - r3
(r2, x3, z3) = solve([eq1, eq2, eq3], (r2, x3, z3))[1]

   (3*sqrt(33)/17 + 39/17, 8*sqrt(3)/5, -2*sqrt(33)/5)

中球の直径は 2(3√33 + 39)/17  = 6.615727992895775 寸である。

2(3√33 + 39)/17

   6.615727992895775

算額の「答」は「中球径七寸二分」となっているが，これは中球と小球の 1 個が大球の直径上に並ぶ解（12 尺 = 7.2 + 4.8）で，残りの 2 個の小球が入る余地がない。「術」の記述はない。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r3) = (120, 48) .// 20
   (r2, x3, z3) = (3*sqrt(33)/17 + 39/17, 8*sqrt(3)/5, -2*sqrt(33)/5)
   plot()
   circle(0, 0, r1, :blue)
   circle(0, r1 - r2, r2, :orange)
   circle(x3, z3, r3, :brown)
   if more        
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, r1, " r1", :blue, :center, :bottom, delta=delta/2)
       point(0, r1 - r2, "中球:r2,(0,0,r1-r2)", :orange, :center, delta=-delta/2)
       point(x3, z3, "小球:r3,(x3,0,z3)", :brown, :center, delta=-delta/2)
   end
end;

function draw2(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r3) = (120, 48) .// 20
   (r2, x3, z3) = (3*sqrt(33)/17 + 39/17, 8*sqrt(3)/5, -2*sqrt(33)/5)
   plot()
   circle(0, 0, r1, :blue)
   rotate(x3, 0, r3, :brown)
   (x, y) = x3*cosd(120), x3*sind(120)
   segment(x, y, x3, 0, :gray90)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2    names = Char["甲乙丙丁戊己庚辛壬癸"...]
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, r1, " r1", :blue, :center, :bottom, delta=delta/2)
       point(x3, 0, "小球:r3,(x3,0,z3)", :brown, :center, delta=-delta/2)
       point(x, y, "", :brown)
   end
end;

算額（その871）

奈良県大和郡山市 庚申堂 明治13年(1880)
http://www.wasan.jp/nara/kosindo.html

牧下英世：数学教育を通して取り組んだ総合的な学習とその実証的な研究-算額を―算額を用いた課題学習とそのフィールドワークの実践から―，2002筑波大学附属駒場論集第42集
https://tsukuba.repo.nii.ac.jp/record/6466/files/13.pdf

大円と小円が交差してできる隙間に甲円から始まる累円を入れる。
大円，小円，甲円の直径をそれぞれ 7 尺 2 寸，6 尺 1 寸，1 尺 7 寸としたとき，乙円，丙円，丁円，戊円の直径を求めよ。

大円の半径と中心座標を R1, (0, 0)
小円の半径と中心座標を R2, (0, 2r1 - R1 + R2)
甲円の半径と中心座標を r1, (0, r1 - R1)
乙円の半径と中心座標を r2, (x2, y2)
丙円の半径と中心座標を r3, (x3, y3)
:

include("julia-source.txt");

using SymPy
@syms R1, R2, r1, r2, x2, y2

(R1, R2, r1) = (72, 61, 17) .// 2
eq1 = x2^2 + y2^2 - (R1 -r2)^2
eq2 = x2^2 + (2r1 - R1 + R2 - y2)^2 - (R2 + r2)^2
eq3 = x2^2 + (y2 - r1 + R1)^2 - (r1 + r2)^2
#(r2, x2, y2) = 
solve([eq1, eq2, eq3], (r2, x2, y2))[2]

   (36465/4681, 204*sqrt(130845)/4681, -109509/4681)

漸化式的に累円のパラメータを数式で求めることが SymPy では困難なので，関数内で solve() を使う，半自動的なやり方を取る。
一つの累円のパラメータが得られたら，それを関数の引数に指定して，次の累円のパラメータを得る。
注意点として（Julia の SymPy 特有であるが），xx/yy の分数は xx//yy にすることと，sqrt(zz) は sqrt(Sym(zz)) にすること。そのようにしなくても良いが，処理時間がかかる。

function nextcircle(R1, R2, r1, r2, x2, y2)
   @syms r3, x3, y3
   eq4 = x3^2 + y3^2 - (R1 -r3)^2
   eq5 = x3^2 + (2r1 - R1 + R2 - y3)^2 - (R2 + r3)^2
   eq6 = (x3 - x2)^2 + (y3 - y2)^2 - (r2 + r3)^2;
   solve([eq4, eq5, eq6], (r3, x3, y3))
end;

# r3
nextcircle(R1, R2, r1, 36465//4681, 204*sqrt(Sym(130845))/4681, -109509//4681)

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (8690825/1404066, 50932*sqrt(130845)/702033, -19854559/1404066)
    (17/2, 0, -55/2)

# r4
nextcircle(R1, R2, r1, 8690825//1404066, 50932*sqrt(Sym(130845))/702033, -19854559//1404066)

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (18641819625/4108026529, 353486916*sqrt(130845)/4108026529, -18850643421/4108026529)
    (36465/4681, 204*sqrt(130845)/4681, -109509/4681)

# r5
nextcircle(R1, R2, r1, 18641819625//4108026529, 353486916*sqrt(Sym(130845))/4108026529, -18850643421//4108026529)

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (4442967010625/1379049831714, 62216188328*sqrt(130845)/689524915857, 4167487120889/1379049831714)
    (8690825/1404066, 50932*sqrt(130845)/702033, -19854559/1404066)

# r6
nextcircle(R1, R2, r1, 4442967010625//1379049831714, 62216188328*sqrt(Sym(130845))/689524915857, 4167487120889//1379049831714)

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (9530164237790625/4195069355668441, 378487752059964*sqrt(130845)/4195069355668441, 35723160673770891/4195069355668441)
    (18641819625/4108026529, 353486916*sqrt(130845)/4108026529, -18850643421/4108026529)

# r7
nextcircle(R1, R2, r1, 9530164237790625//4195069355668441, 378487752059964*sqrt(Sym(130845))/4195069355668441, 35723160673770891//4195069355668441)

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (2271355810006765625/1413029171738162306, 62689304552989212*sqrt(130845)/706514585869081153, 17460791512813260881/1413029171738162306)
    (4442967010625/1379049831714, 62216188328*sqrt(130845)/689524915857, 4167487120889/1379049831714)

# r8
nextcircle(R1, R2, r1, 2271355810006765625//1413029171738162306, 62689304552989212*sqrt(Sym(130845))/706514585869081153, 17460791512813260881//1413029171738162306)

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (4872058212464512265625/4255498594259851496689, 369959068275411941556*sqrt(130845)/4255498594259851496689, 63967589464505474522739/4255498594259851496689)
    (9530164237790625/4195069355668441, 378487752059964*sqrt(130845)/4195069355668441, 35723160673770891/4195069355668441)

累円の直径と中心座標は以下のようになる。算額の答えとはずいぶん異なる。

乙円: 直径 = 15.58000, (15.7641, -23.3944)
丙円: 直径 = 12.37951, (26.2429, -14.1408)
丁円: 直径 =  9.07580, (31.1257, -4.58873)
戊円: 直径 =  6.44352, (32.6386,  3.02200)
己円: 直径 =  4.54351, (32.6356,  8.51551)
庚円: 直径 =  3.21487, (32.0960, 12.35700)
辛円: 直径 =  2.28977, (31.4472, 15.03170)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   names = Char["甲乙丙丁戊己庚辛壬癸"...]
   (R1, R2, r1) = (72, 61, 17) .// 2
   plot(showaxis=false)
   delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2    names = Char["甲乙丙丁戊己庚辛壬癸"...]
   circlef(0, 0, R1, :lightgreen)
   circlef(0, 2r1 - R1 + R2, R2, :cadetblue1)
   circle(0, 2r1 - R1 + R2, R2, :lightslateblue)
   circle(0, 0, R1, :mediumseagreen)
   circlef(0, r1 - R1, r1, :gold)
   number = 1
   for (r, x, y) in [
       (7.790002136295663, 15.764133064156171, -23.394360179448835)
       (6.189755324892134, 26.242896581838256, -14.140759052637128)
       (4.537901470061319, 31.12566720233952, -4.588734587745892)
       (3.221759582902747, 32.63863611252851, 3.021998933649333)
       (2.2717536779012537, 32.63557363626892, 8.515511340831878)
       (1.607437309459633, 32.095998094235, 12.356992949646468)
       (1.1448854005113114, 31.447186145793232, 15.031749640521548)]
       number += 1
       circlef(x, y, r, number)
       circlef(-x, y, r, number)
       point(x, y, names[number], :white, :center, :vcenter, mark=false)
       @printf("%s円: 直径 = %8.5f, (%g, %g)\n", names[number], 2r, x, y)
   end
   if more        
       #hline!([0], color=:gray80, lw=0.5)
       #vline!([0], color=:gray80, lw=0.5)
       point(0, 0, "大円:R1,(0,0)", :red, :center, delta=-1)
       point(0, 2r1 - R1 + R2, "小円:R2,(0,2r1-R1+R2)", :green, :center, delta=-1)
       point(0, r1 - R1, " 甲円:r1\n(0,r1-R1)", :white, :center, delta=-1)
   end
end;

算額（その870）

奈良県大和郡山市 庚申堂 明治13年(1880)
http://www.wasan.jp/nara/kosindo.html

牧下英世：数学教育を通して取り組んだ総合的な学習とその実証的な研究―算額を用いた課題学習とそのフィールドワークの実践から―，2002筑波大学附属駒場論集第42集
https://tsukuba.repo.nii.ac.jp/record/6466/files/13.pdf

長方形内に大円，中円，小円を入れる。中円と小円の直径がそれぞれ 4 寸 5 分，2 寸，長方形の長辺と短辺の和が 2 尺 1 寸 2 分 5 厘のとき大円の直径と長方形の長辺と短辺を求めよ。

長方形の長辺と短辺の長さを a, b
大円の半径と中心座標を r1, (r1, r1)
中円の半径と中心座標を r2, (a - r2, r2)
小円の半径と中心座標を r3, (r3, b - r3)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a, b, r1, r2, r3, K
(r2, r3, K) = (45//20, 2//2, 2125//100)
eq1 = (a + b) - K
eq2 = (a - r2 - r1)^2 + (r1 - r2)^2 - (r1 + r2)^2 |> expand
eq3 = (r1 - r3)^2 + (b - r3 - r1)^2 - (r1 + r3)^2 |> expand
res = solve([eq1, eq2, eq3], (r1, a, b))[2]  # 4 組のうち 2 番目

   (4, 49/4, 9)

大円の直径は 8 寸，長方形の長辺と短辺は 12.25 寸と 9 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, r3, K) = (45//20, 2//2, 2125//100)
   (r1, a, b) = (4, 49/4, 9)
   plot([0, a, a, 0, 0], [0, 0, b, b, 0], color=:blue, lw=0.5)
   circle(r1, r1, r1)
   circle(a - r2, r2, r2, :green)
   circle(r3, b - r3, r3, :magenta)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2    names = Char["甲乙丙丁戊己庚辛壬癸"...]
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(0, b, " b", :blue, :left, :bottom, delta=delta/2)
       point(r1, r1, "大円:r1,(r1,r1)", :red, :center, delta=-delta/2)
       point(a - r2, r2, "中円:r2,(a-r2,r2)", :green, :center, delta=-delta/2)
       point(r3, b - r3, " 小円:r3,(r3,b-r3)", :magenta, :left, :bottom, delta=delta/2)
   end
end;

算額（その869）

奈良県大和郡山市 庚申堂 明治13年(1880)
http://www.wasan.jp/nara/kosindo.html

牧下英世：数学教育を通して取り組んだ総合的な学習とその実証的な研究-算額を用いた課題学習とそのフィールドワークの実践から-，2002筑波大学附属駒場論集第42集
https://tsukuba.repo.nii.ac.jp/record/6466/files/13.pdf

直角三角形内に斜線を引き，2 個の等円を入れる。直角三角形の底辺（股），高さ（鈎）がそれぞれ 4 寸，3 寸のとき，等円の直径と斜線の長さを求めよ。

鈎，股 を b, a
斜線と股の交点座標を (c, 0)
等円の半径と中心座標を r, (r, r), (x, r)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms d, a, b, c, r, x
eq1 = numerator(apart(dist(a, 0, 0, b, x, r) - r^2, d))
eq2 = numerator(apart(dist(c, 0, 0, b, x, r) - r^2, d))
eq3 = (b + c - 2r)^2 - (b^2 + c^2);  # b + c - sqrt(b^2 + c^2) - 2r
(c, x, r) = solve([eq1, eq2, eq3], (c, x, r))[8]  # 8 組中 8 番目
c |> println
x |> println
r |> println

   sqrt(b*(-a + sqrt(a^2 + b^2)))*(a - b + sqrt(a^2 + b^2))/(2*b)
   (a^2*b - a^2*sqrt(b*(-a + sqrt(a^2 + b^2))) - a*b^2/2 + a*b*sqrt(b*(-a + sqrt(a^2 + b^2)))/2 - a*b*sqrt(a^2 + b^2) + a*sqrt(b*(-a + sqrt(a^2 + b^2)))*sqrt(a^2 + b^2) + b^3/2 - b^2*sqrt(b*(-a + sqrt(a^2 + b^2)))/2 - b^2*sqrt(a^2 + b^2)/2 + b*sqrt(b*(-a + sqrt(a^2 + b^2)))*sqrt(a^2 + b^2)/2)/(a*b - 2*a*sqrt(b*(-a + sqrt(a^2 + b^2))) + b^2 - b*sqrt(a^2 + b^2))
   b/2 - sqrt(-a*b/4 + b*sqrt(a^2 + b^2)/4)

等円の直径は，2r = 1.2679491924311228 寸

2r(a => 4, b => 3) |> N

   1.2679491924311228

斜線の長さは，sqrt(b^2 + c^2) = 3.4641016151377544 寸

sqrt(b^2 + c^2)(a => 4, b => 3) |> N

   3.4641016151377544

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b) = (4, 3)
   c = sqrt(b*(-a + sqrt(a^2 + b^2)))*(a - b + sqrt(a^2 + b^2))/(2*b)
   x = (a^2*b - a^2*sqrt(b*(-a + sqrt(a^2 + b^2))) - a*b^2/2 + a*b*sqrt(b*(-a + sqrt(a^2 + b^2)))/2 - a*b*sqrt(a^2 + b^2) + a*sqrt(b*(-a + sqrt(a^2 + b^2)))*sqrt(a^2 + b^2) + b^3/2 - b^2*sqrt(b*(-a + sqrt(a^2 + b^2)))/2 - b^2*sqrt(a^2 + b^2)/2 + b*sqrt(b*(-a + sqrt(a^2 + b^2)))*sqrt(a^2 + b^2)/2)/(a*b - 2*a*sqrt(b*(-a + sqrt(a^2 + b^2))) + b^2 - b*sqrt(a^2 + b^2))
   r = b/2 - sqrt(-a*b/4 + b*sqrt(a^2 + b^2)/4)
   plot([0, a, 0, 0], [0, 0, b, 0], color=:blue, lw=0.5)
   circle(r, r, r)
   circle(x, r, r)
   segment(c, 0, 0, b, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2    names = Char["甲乙丙丁戊己庚辛壬癸"...]
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, "a", :blue, :left, :bottom, delta=delta/2)
       point(c, 0, "c ", :blue, :right, :bottom, delta=delta/2)
       point(0, b, "b", :blue, :left, :bottom, delta=delta/2)
       point(r, r, "等円:r,(r,r)", :red, :center, delta=-delta/2)
       point(x, r, "等円:r,(x,r)", :red, :center, delta=-delta/2)
   end
end;

算額（その868）

奈良県大和郡山市 庚申堂 明治13年(1880)
http://www.wasan.jp/nara/kosindo.html

牧下英世：数学教育を通して取り組んだ総合的な学習とその実証的な研究-算額を―算額を用いた課題学習とそのフィールドワークの実践から―，2002筑波大学附属駒場論集第42集
https://tsukuba.repo.nii.ac.jp/record/6466/files/13.pdf

"たばや"の算額
https://www.libe.nara-k.ac.jp/~yano/ketcindy/sangaku_tabaya.html

大円の中に，甲円と乙円を入れる。大円に接し，甲円と乙円に外接する丙円を描く。次に，大円に接し，甲円と丙円に外接する丁円を描く。同じ手順で，戊円，己円...を描くことができる。大円，甲円の直径がそれぞれ 16 寸，9.6 寸のとき，乙円，丙円，丁円の直径を求めよ。

大円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, r1 - R)
乙円の半径と中心座標を r2, (x2, y2); x2 = r2
丙円の半径と中心座標を r3, (x3, y3)
丁円の半径と中心座標を r4, (x4, x5)
とおき，以下のように方程式を解いてゆく。

1.　乙円の半径と中心座標を求める

大円と甲円の半径が既知なので，乙円の半径と中心座標は次の二元連立方程式を解けばよい。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive,
     r2::positive, x2::positive, y2::positive

x2 = r2
eq1 = r2^2 + y2^2 - (R - r2)^2
eq2 = r2^2 + (y2 - r1 + R)^2 - (r1 + r2)^2
res1 = solve([eq1, eq2], (r2, y2))[1]

   (-(-R + r1)*(R + (-R^2 + 3*R*r1)/(R + r1))/(R + r1), (-R^2 + 3*R*r1)/(R + r1))

2.　丙円の半径と中心座標を求める

乙円までは半径と中心座標が決まったので，次の累円（丙円）の半径と中心座標は次の三元連立方程式を解けばよい。

@syms r3::positive, x3::positive, y3::real

eq3 = x3^2 + y3^2 - (R - r3)^2
eq4 = x3^2 + (y3 - r1 + R)^2 - (r1 +r3)^2
eq5 = (x2 - x3)^2 + (y2 - y3)^2 - (r2 + r3)^2;
res2 = solve([eq3, eq4, eq5], (r3, x3, y3));
# res2[1]

2 組の解が得られるが，2 番目のものが適解である。
求める累円の前にある累円（甲円）の半径と中心座標から，求めるべき累円（乙円）の半径と中心座標が得られる。
この関係式は前の累円と次の累円の関係式なので，次々に適用することで，累円の半径と中心座標を決定していくことができる。

3.　丙円以降の半径と中心座標を求める

これを関数にすると以下のようなものになる。

nextcircle(R, r1, r2, x2, y2) = ((R^6 - R^5*r1 + R^5*r2 + 3*R^5*y2 - R^4*r1^2 - R^4*r1*r2 - R^4*r1*y2 - R^4*r2^2 + 2*R^4*r2*y2 + R^4*x2^2 + 3*R^4*y2^2 + R^3*r1^3 - R^3*r1^2*r2 - 3*R^3*r1^2*y2 + R^3*r1*r2^2 - 2*R^3*r1*r2*y2 + 3*R^3*r1*x2^2 + R^3*r1*y2^2 - R^3*r2^3 - R^3*r2^2*y2 + R^3*r2*x2^2 + R^3*r2*y2^2 + R^3*x2^2*y2 + R^3*y2^3 - 2*R^2*sqrt(r1)*x2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + R^2*r1^3*r2 + R^2*r1^3*y2 + R^2*r1^2*r2^2 - 2*R^2*r1^2*r2*y2 - R^2*r1^2*x2^2 - 3*R^2*r1^2*y2^2 + R^2*r1*r2^3 - R^2*r1*r2^2*y2 - R^2*r1*r2*x2^2 - R^2*r1*r2*y2^2 + R^2*r1*x2^2*y2 + R^2*r1*y2^3 - R*r1^3*r2^2 + 2*R*r1^3*r2*y2 - 3*R*r1^3*x2^2 - R*r1^3*y2^2 + R*r1^2*r2^3 + R*r1^2*r2^2*y2 - R*r1^2*r2*x2^2 - R*r1^2*r2*y2^2 - R*r1^2*x2^2*y2 - R*r1^2*y2^3 + 2*r1^(5/2)*x2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) - r1^3*r2^3 + r1^3*r2^2*y2 + r1^3*r2*x2^2 + r1^3*r2*y2^2 - r1^3*x2^2*y2 - r1^3*y2^3)/(2*(R^5 - R^4*r1 + 2*R^4*r2 + 2*R^4*y2 - R^3*r1^2 - 2*R^3*r1*r2 + 2*R^3*r1*y2 + R^3*r2^2 + 2*R^3*r2*y2 + R^3*y2^2 + R^2*r1^3 - 2*R^2*r1^2*r2 - 2*R^2*r1^2*y2 - R^2*r1*r2^2 + 2*R^2*r1*r2*y2 + 4*R^2*r1*x2^2 + 3*R^2*r1*y2^2 + 2*R*r1^3*r2 - 2*R*r1^3*y2 - R*r1^2*r2^2 - 2*R*r1^2*r2*y2 + 4*R*r1^2*x2^2 + 3*R*r1^2*y2^2 + r1^3*r2^2 - 2*r1^3*r2*y2 + r1^3*y2^2)), (R^3*sqrt(r1)*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + 2*R^3*r1^2*x2 - 2*R^3*r1*r2*x2 + 2*R^3*r1*x2*y2 + R^2*sqrt(r1)*r2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + R^2*sqrt(r1)*y2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + 2*R^2*r1^3*x2 - 2*R^2*r1*r2^2*x2 + 2*R^2*r1*x2^3 + 2*R^2*r1*x2*y2^2 - R*r1^(5/2)*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + 2*R*r1^(3/2)*y2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + 2*R*r1^3*r2*x2 - 2*R*r1^3*x2*y2 - 2*R*r1^2*r2^2*x2 + 2*R*r1^2*x2^3 + 2*R*r1^2*x2*y2^2 - r1^(5/2)*r2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)) + r1^(5/2)*y2*sqrt(R*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 - 2*R^2*r1*r2 - 2*R^2*r1*y2 + 4*R^2*r2*y2 + 2*R*r1*r2^2 - 4*R*r1*r2*y2 + 2*R*r1*x2^2 + 2*R*r1*y2^2 - 2*R*r2^3 + 2*R*r2^2*y2 + 2*R*r2*x2^2 + 2*R*r2*y2^2 - 2*R*x2^2*y2 - 2*R*y2^3 + 2*r1*r2^3 - 2*r1*r2^2*y2 - 2*r1*r2*x2^2 - 2*r1*r2*y2^2 + 2*r1*x2^2*y2 + 2*r1*y2^3 - r2^4 + 2*r2^2*x2^2 + 2*r2^2*y2^2 - x2^4 - 2*x2^2*y2^2 - y2^4)))/(R^5 - R^4*r1 + 2*R^4*r2 + 2*R^4*y2 - R^3*r1^2 - 2*R^3*r1*r2 + 2*R^3*r1*y2 + R^3*r2^2 + 2*R^3*r2*y2 + R^3*y2^2 + R^2*r1^3 - 2*R^2*r1^2*r2 - 2*R^2*r1^2*y2 - R^2*r1*r2^2 + 2*R^2*r1*r2*y2 + 4*R^2*r1*x2^2 + 3*R^2*r1*y2^2 + 2*R*r1^3*r2 - 2*R*r1^3*y2 - R*r1^2*r2^2 - 2*R*r1^2*r2*y2 + 4*R*r1^2*x2^2 + 3*R*r1^2*y2^2 + r1^3*r2^2 - 2*r1^3*r2*y2 + r1^3*y2^2), -sqrt(r1)*x2*sqrt(-R*(-R^2 - 2*R*r2 - r2^2 + x2^2 + y2^2)*(R^2 - 2*R*r1 + 2*R*y2 + 2*r1*r2 - 2*r1*y2 - r2^2 + x2^2 + y2^2))*(R + r1)/(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 + R^2*r1^2 - 4*R^2*r1*r2 + R^2*r2^2 + 2*R^2*r2*y2 + R^2*y2^2 + 2*R*r1^2*r2 - 2*R*r1^2*y2 - 2*R*r1*r2^2 + 4*R*r1*x2^2 + 2*R*r1*y2^2 + r1^2*r2^2 - 2*r1^2*r2*y2 + r1^2*y2^2) + (-R^5 + 4*R^4*r1 - 3*R^4*r2 - R^4*y2 - 3*R^3*r1^2 + 8*R^3*r1*r2 + 2*R^3*r1*y2 - 3*R^3*r2^2 - 2*R^3*r2*y2 + R^3*x2^2 + R^3*y2^2 - 5*R^2*r1^2*r2 + 3*R^2*r1^2*y2 + 4*R^2*r1*r2^2 - 4*R^2*r1*x2^2 - R^2*r2^3 - R^2*r2^2*y2 + R^2*r2*x2^2 + R^2*r2*y2^2 + R^2*x2^2*y2 + R^2*y2^3 - R*r1^2*r2^2 + 2*R*r1^2*r2*y2 + 3*R*r1^2*x2^2 - R*r1^2*y2^2 - 2*R*r1*r2^2*y2 + 2*R*r1*x2^2*y2 + 2*R*r1*y2^3 + r1^2*r2^3 - r1^2*r2^2*y2 - r1^2*r2*x2^2 - r1^2*r2*y2^2 + r1^2*x2^2*y2 + r1^2*y2^3)/(2*(R^4 - 2*R^3*r1 + 2*R^3*r2 + 2*R^3*y2 + R^2*r1^2 - 4*R^2*r1*r2 + R^2*r2^2 + 2*R^2*r2*y2 + R^2*y2^2 + 2*R*r1^2*r2 - 2*R*r1^2*y2 - 2*R*r1*r2^2 + 4*R*r1*x2^2 + 2*R*r1*y2^2 + r1^2*r2^2 - 2*r1^2*r2*y2 + r1^2*y2^2)));

順次適用した結果を表示すると以下のようになる。
大円，甲円の直径がそれぞれ 16 寸，9.6 寸 なので，乙円の，半径と中心座標は以下のようになる。

res1

   (-(-R + r1)*(R + (-R^2 + 3*R*r1)/(R + r1))/(R + r1), (-R^2 + 3*R*r1)/(R + r1))

res1[1](R => 16/2, r1 => 9.6/2) |> N  # r2 = x2

   3.0

res1[2](R => 16/2, r1 => 9.6/2) |> N  # y2

   3.999999999999999

nextcircle(16/2, 9.6/2, 3, 3, 4)  # r3, x3, y3

   (2.0000000000000004, 5.999999999999999, 0.0)

nextcircle(16/2, 9.6/2, 2, 6, 0)  # r4, x4, y4

   (1.2000000000000002, 6.000000000000001, -3.2000000000000006)

nextcircle(16/2, 9.6/2, 1.2, 6, -3.2) # r5, x5, y5

   (0.7499999999999988, 5.250000000000001, -4.999999999999999)

nextcircle(16/2, 9.6/2, 0.75, 5.25, -5)  # r6, x6, y6

   (0.5000000000000001, 4.499999999999999, -6.000000000000001)

乙円，丙円，丁円の直径は 2r2 = 6 寸, 2r3 = 4　寸, 2r4 = 2.4 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, r1) = (160, 96) .// 20
   (r2, y2) = (-(-R + r1)*(R + (-R^2 + 3*R*r1)/(R + r1))/(R + r1), (-R^2 + 3*R*r1)/(R + r1))
   x2 = r2
   plot(showaxis=false)
   delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2    names = Char["甲乙丙丁戊己庚辛壬癸"...]
   circlef(0, 0, R, :orange)
   circlef(0, r1 - R, r1, :purple)
   names = Char["甲乙丙丁戊己庚辛壬癸"...]
   @printf("%g %g %g %g\n", 1, r1, 0, r1 - R)
   for i = 2:15
       @printf("%g %g %g %g\n", i, r2, x2, y2)
       if i <= 8
           notation = @sprintf("%s円:r%g,(x%g,y%g)", names[i], i, i, i)
           point(x2, y2, names[i], :white, :center, :vcenter)
       end
       circlef(x2, y2, r2, i)
       circlef(-x2, y2, r2, i)
       r2, x2, y2 = nextcircle(R, r1, r2, x2, y2)
   end

   if more        
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 0, "大円:R,(0,0)", :white, :center, delta=-2delta)
       point(0, r1 - R, "甲円:r1,(0,r1-R)", :white, :center, delta=-2delta)
   end
end;

   1 4.8 0 -3.2
   2 3 3 4
   3 2 6 0
   4 1.2 6 -3.2
   5 0.75 5.25 -5
   6 0.5 4.5 -6
   7 0.352941 3.88235 -6.58824
   8 0.26087 3.3913 -6.95652
   9 0.2 3 -7.2
   10 0.157895 2.68421 -7.36842
   11 0.12766 2.42553 -7.48936
   12 0.105263 2.21053 -7.57895
   13 0.0882353 2.02941 -7.64706
   14 0.075 1.875 -7.7
   15 0.0645161 1.74194 -7.74194

4.　直径だけを求める場合

累円の直径（半径）だけを逐次求めるには，算法助術の公式55 を使えばよい。

using SymPy
@syms d1, d2, d3, d4, R, r1, r2, r3, r4
(d1, d2, d3) = (R, r1, r2)
eq55 = d1^2*d2^2*d3^2 + d1^2*d4^2*(d2 - d3)^2 + 2*d1*d2^2*d3^2*d4 - 2*d1*d2*d3*d4*(d1 - d4)*(d2 + d3) + d2^2*d3^2*d4^2;

外円 R に内接し，甲円 r1 と i 番目の累円 r(i)に接する r(i+1) 番目の累円の半径 d4 は，eq55 を 解けば求めることができる。

res = solve(eq55, d4)[1]
res |> println

   (R*r1*r2*(R*r1 + R*r2 - r1*r2) - 2*sqrt(-R^3*r1^3*r2^3*(-R + r1 + r2)))/(R^2*r1^2 - 2*R^2*r1*r2 + R^2*r2^2 + 2*R*r1^2*r2 + 2*R*r1*r2^2 + r1^2*r2^2)

これを関数にすれば，（外円，甲円と）乙円を初期値として，次の円の半径を求めることができる。

nxt(R, r1, r2) = (R*r1*r2*(R*r1 + R*r2 - r1*r2) - 2*sqrt(-R^3*r1^3*r2^3*(-R + r1 + r2)))/(R^2*r1^2 - 2*R^2*r1*r2 + R^2*r2^2 + 2*R*r1^2*r2 + 2*R*r1*r2^2 + r1^2*r2^2);

(R, r1) = (160, 96) .// 20
r = 3  # r2 から始める
for i = 2:15
   @printf("%g %g\n", i, r)
   r = nxt(R, r1, r)  # i = 2 のとき r3 が求まる
end

   2 3
   3 2
   4 1.2
   5 0.75
   6 0.5
   7 0.352941
   8 0.26087
   9 0.2
   10 0.157895
   11 0.12766
   12 0.105263
   13 0.0882353
   14 0.075
   15 0.0645161

算額（その867）

奈良県橿原市木原町 耳成山口神社（天神社） 嘉永7年(1854)
http://www.wasan.jp/nara/miminasi.html

牧下英世：数学教育を通して取り組んだ総合的な学習とその実証的な研究-算額を―算額を用いた課題学習とそのフィールドワークの実践から―，2002筑波大学附属駒場論集第42集
https://tsukuba.repo.nii.ac.jp/record/6466/files/13.pdf

外円内に甲円，乙円，丙円，丁円が互いに内接・外接して入っている。甲円，丁円の直径がそれぞれ 5 尺 2 寸，7 寸のとき，外円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, R - r1)
乙円の半径と中心座標を r2, (0, r2 - R)
丙円の半径と中心座標を r3, (x3, y3)
丁円の半径と中心座標を r4, (x4, y4)
とおき，以下の連立方程式を解く。

eq0 は算法助術の公式55 であるが，この問題では r2 = R - r1 なので eq1 のように簡単になる。
なお，デカルトの円定理による条件式 eq00 を使うこともできるが SymPy では解けない（数値解を求めることはできる）。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, r2::positive, r3::positive, r4::positive,
     x3::positive, y3::negative, x4::positive, y4::negative,
     d1::positive, d2::positive, d3::positive, d4::positive

# (k1, k2, k3, k4) = 1.0 ./ (r1, r2, r3, -R)
# eq00 = 1/(-(k1 + k2 + k3) + 2sqrt(k1*k2 + k2*k3 + k3*k1)) - R

(r1, r4) = (52, 7) .// 2
r2 = R - r1
(d1, d2, d3, d4) = (R, r1, r2, r3)
eq0 = d1^2*d2^2*d3^2 + d1^2*d4^2*(d2 - d3)^2 + 2*d1*d2^2*d3^2*d4 - 2*d1*d2*d3*d4*(d1 - d4)*(d2 + d3) + d2^2*d3^2*d4^2
eq1 = -R^2*r1 + R^2*r3 + R*r1^2 - R*r1*r3 + r1^2*r3
eq2 = x3^2 + y3^2 - (R - r3)^2 |> expand
eq3 = x4^2 + y4^2 - (R - r4)^2 |> expand
eq4 = x3^2 + (r2 - R - y3)^2 - (r2 + r3)^2 |> expand
eq5 = x4^2 + (r2 - R - y4)^2 - (r2 + r4)^2 |> expand
eq6 = (x3 - x4)^2 + (y3 - y4)^2 - (r3 + r4)^2 |> expand
res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (R, r3, x3, y3, x4, y4))

   1-element Vector{NTuple{6, Sym{PyCall.PyObject}}}:
    (13 + 13*sqrt(785)/15, 728/73, 1456/73, -13 - 221*sqrt(785)/1095, 14, -19*sqrt(785)/30 - 13)

甲円，丁円の直径がそれぞれ 5 尺 2 寸，7 寸のとき，外円の直径は 2(13 + 13√785/15) = 74.56427585055592 寸である。

2(13 + 13√785/15)

   74.56427585055592

その他のパラメータは以下のとおりである。

r1 = 26;  r4 = 3.5;  R = 37.2821;  r2 = 11.2821;  r3 = 9.9726;  x3 = 19.9452;  y3 = -18.6547;  x4 = 14;  y4 = -30.7446

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r4) = (26, 3.5)
   (R, r3, x3, y3, x4, y4) = 13 .* (1 + √785/15, 56/73, 112/73, -1 - 17√785/1095, 14/13, -1 - 19√785/390)
   r2 = R - r1
   @printf("r1 = %g;  r4 = %g;  R = %g;  r2 = %g;  r3 = %g;  x3 = %g;  y3 = %g;  x4 = %g;  y4 = %g\n", r1, r4, R, r2, r3, x3, y3, x4, y4)
   plot()
   circle(0, 0, R)
   circle(0, R - r1, r1, :green)
   circle(0, r2 - R, r2, :magenta)
   circle2(x3, y3, r3, :blue)
   circle2(x4, y4, r4, :brown)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R - r1, "甲円:r1,(0,R-r1)", :green, :center, delta=-delta/2)
       point(0, r2 - R, "乙円:r2,(0,r2-R)", :magenta, :center, delta=-delta/2)
       point(x3, y3, "丙円:r3,(x3,y3)", :blue, :center, delta=-delta/2)
       point(x4, y4, " 丁円:r4,(x4,y4)", :black, :left, :vcenter)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
   end
end;

算額（その866）

岩手県平泉町　中尊寺阿弥陀堂（中尊寺地蔵院にて保管） 安政6年(1859)
http://www.wasan.jp/iwate/chusonji3.html

牧下英世：数学史を取り入れた授業実践―算額の教材化と総合的な学習―，2000筑波大学附属駒場論集第40集
https://tsukuba.repo.nii.ac.jp/record/6486/files/10.pdf

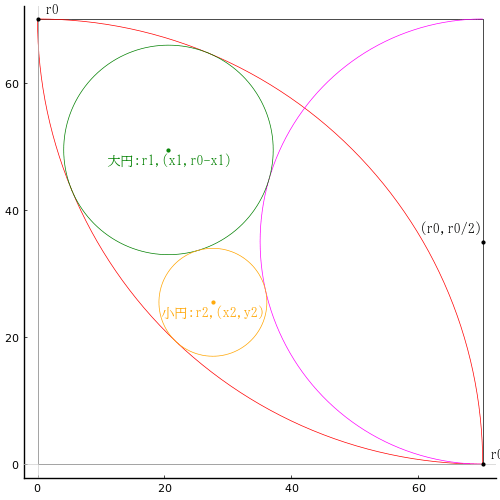
正方形内に対角線（角斜）と 1 本の斜線（甲斜）を引き，区分された領域に四分円，乙円，丙円，丁円，戊円，己円を入れる。正方形の一辺の長さが与えられたとき，甲斜の長さと乙円，丙円，丁円，戊円，己円の直径の和を求めよ。

正方形の一辺の長さを a
甲斜と正方形の辺の交点座標を (0, b)
半円の半径と中心座標を r0, (r0, a)
乙円の半径と中心座標を r1, (r0, a - r1)
丙円の半径と中心座標を r2, (a - r2, y2)
丁円の半径と中心座標を r3, (x3, r3)
戊円の半径と中心座標を r4, (r4, y4)
己円の半径と中心座標を r5, (a - r5, y5)
とおき，以下の連立方程式を解く。
SymPy の能力的に，一度に自動的に解くことができないので，手動で逐次解いていく。

include("julia-source.txt");

using SymPy
@syms a::positivev, b::positice, r0::positive,
     r1::positive, r2::positive, y2::positive,
     r3::positive, x3::positice,  r4::positive,
     y4::positive, r5::positice, y5::positice, d
s2 = √Sym(2)
r1 = r0/2
eq1 = numerator(apart(dist(0, 0, a, a, r0, a) - r0^2, d))
eq2 = numerator(apart(dist(0, 0, a, a, a - r2, y2) - r2^2, d))
eq3 = numerator(apart(dist(0, 0, a, a, x3, r3) - r3^2, d))
eq4 = numerator(apart(dist(0, 0, a, a, r4, y4) - r4^2, d))
eq5 = numerator(apart(dist(0, b, a, 0, r0, a) - r0^2, d))
eq6 = numerator(apart(dist(0, b, a, 0, a - r2, y2) - r2^2, d))
eq7 = numerator(apart(dist(0, b, a, 0, x3, r3) - r3^2, d))
eq8 = numerator(apart(dist(0, b, a, 0, r4, y4) - r4^2, d))
eq9 = numerator(apart(dist(0, b, a, 0, a - r5, y5) - r5^2, d))
eq10 = (r2 - r5)^2 + (y2 - y5)^2 - (r2 + r5)^2 |> expand;

1.　eq1, eq5 から r0, b を求める。

res_r0 = solve(eq1, r0)[1]  # r0 確定
res_r0 |> println
res_r0(a => 1.5) |> N  # 0.6213203435596426

   a*(-1 + sqrt(2))

   0.6213203435596426

res_b = solve(eq5(r0 => res_r0), b)[1]  # b 確定
res_b |> println
res_b(a => 1.5) |> N  # 1.2016314489305129

   -3*a*sqrt(20 - 14*sqrt(2)) - 2*sqrt(2)*a*sqrt(20 - 14*sqrt(2)) + sqrt(2)*a + 2*a

   1.201631448930513

2.　eq2, eq6 から y2, r2 を求める。

res_r2 = solve(eq2, r2)[2]
res_r2 |> println

   -a + y2 + sqrt(2)*(a - y2)

eq16 = eq6(b => res_b, r2 => res_r2) |> expand |> simplify
eq16 |> println

   a^2*(-3*a^2 + 2*sqrt(2)*a^2 - 6*sqrt(2)*a*y2 + 2*a*y2*sqrt(20 - 14*sqrt(2)) + 4*a*y2*sqrt(10 - 7*sqrt(2)) + 6*a*y2 - 2*y2^2 - 4*y2^2*sqrt(10 - 7*sqrt(2)) - 2*y2^2*sqrt(20 - 14*sqrt(2)) + 4*sqrt(2)*y2^2)

res_y2 = solve(eq16, y2)[2]
res_y2 |> println

   a*(-3*sqrt(2) - sqrt(-4*sqrt(2) - 4*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 4*sqrt(10 - 7*sqrt(2)) + 9) + sqrt(20 - 14*sqrt(2)) + 2*sqrt(10 - 7*sqrt(2)) + 3)/(2*(-2*sqrt(2) + sqrt(2)*sqrt(10 - 7*sqrt(2)) + 2*sqrt(10 - 7*sqrt(2)) + 1))

res_y2 = apart(res_y2/a, d)*a |> factor  # y2 確定
res_y2 |> println
res_y2(a => 1.5) |> N  # 0.694654694074625

   a*(-9*sqrt(2) + 9*sqrt(2)*sqrt(10 - 7*sqrt(2)) + 14*sqrt(10 - 7*sqrt(2)) + 20)/34

   0.694654694074625

res_r2 = res_r2(y2 => res_y2) |> simplify  # r2 確定
res_r2 |> println
res_r2(a => 1.5) |> N  # 0.33358494810779965

   a*(-5*sqrt(20 - 14*sqrt(2)) - 4*sqrt(10 - 7*sqrt(2)) + 4 + 5*sqrt(2))/34

   0.33358494810779965

3.　eq3, eq7 から x3，r3 を求める。

res_r3 = solve(eq3, r3)[1]
res_r3 |> println

   x3*(-1 + sqrt(2))

eq17 = eq7(b => res_b, r3 => res_r3) |> expand |> simplify
eq17 |> println

   a^2*(-20*a^2*sqrt(20 - 14*sqrt(2)) - 28*a^2*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2)*a^2 + 10*a^2 - 20*a*x3 - 14*sqrt(2)*a*x3 + 42*a*x3*sqrt(20 - 14*sqrt(2)) + 60*a*x3*sqrt(10 - 7*sqrt(2)) - 28*x3^2*sqrt(10 - 7*sqrt(2)) - 18*x3^2*sqrt(20 - 14*sqrt(2)) + 4*x3^2 + 10*sqrt(2)*x3^2)

res_x3 = apart(solve(eq17, x3)[1]/a, d)*a |> simplify  # x3 確定
res_x3 |> println
res_x3(a => 1.5) |> N  # 0.6882058497807045

   a*(-2*sqrt(10 - 7*sqrt(2)) - sqrt(20 - 14*sqrt(2)) + 2)/2

   0.6882058497807045

res_r3 = res_r3(x3 => res_x3) |> simplify  # r3 確定
res_r3 |> println
res_r3(a => 1.5) |> N  # 0.2850641966836687

   a*(-2 - sqrt(20 - 14*sqrt(2)) + 2*sqrt(2))/2

   0.2850641966836687

4.　eq4, eq8 から y4，r4 を求める。

res_r4 = solve(eq4, r4)[1]
res_r4 |> println

   y4*(-1 + sqrt(2))

eq18 = eq8(b => res_b, r4 => res_r4) |> expand |> simplify
eq18 |> println

   a^2*(-20*a^2*sqrt(20 - 14*sqrt(2)) - 28*a^2*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2)*a^2 + 10*a^2 - 10*sqrt(2)*a*y4 - 8*a*y4 + 22*a*y4*sqrt(20 - 14*sqrt(2)) + 32*a*y4*sqrt(10 - 7*sqrt(2)) - 2*y4^2 - 4*y4^2*sqrt(10 - 7*sqrt(2)) - 2*y4^2*sqrt(20 - 14*sqrt(2)) + 4*sqrt(2)*y4^2)

res_y4 = solve(eq18, y4)[2]
res_y4 |> println

   a*(-5 - 3*sqrt(2) + 14*sqrt(10 - 7*sqrt(2)) + 10*sqrt(20 - 14*sqrt(2)))/(-2*sqrt(2) + sqrt(2)*sqrt(10 - 7*sqrt(2)) + 2*sqrt(10 - 7*sqrt(2)) + 1)

res_y4 = apart(solve(eq18, y4)[2]/a, d)*a |> simplify  # y4 確定
res_y4 |> println
res_y4(a => 1.5) |> N  # 0.6451521645656638

   a*(-78*sqrt(10 - 7*sqrt(2)) - 55*sqrt(20 - 14*sqrt(2)) + 27 + 21*sqrt(2))/17

   0.6451521645656638

res_r4 = res_r4(y4 => res_y4) |> simplify  # r4 確定
res_r4 |> println
res_r4(a => 1.5) |> N  # 0.26723077635745685

   a*(-23*sqrt(20 - 14*sqrt(2)) - 32*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 15)/17

   0.2672307763574568

5.　eq9, eq10 から r5，y5 を求める。

eq19 = eq9(b => res_b) |> simplify
eq19 |> println

   a^2*(-r5^2 - 2*r5*y5*(-3*sqrt(20 - 14*sqrt(2)) - 4*sqrt(10 - 7*sqrt(2)) + sqrt(2) + 2) + y5^2)

res_y5 = solve(eq19, y5)[1]
res_y5 |> println

   r5*(-3*sqrt(20 - 14*sqrt(2)) - 4*sqrt(10 - 7*sqrt(2)) + sqrt(-20*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11) + sqrt(2) + 2)

eqA = eq10(r2 => res_r2, y2 => res_y2, y5 => res_y5) |> simplify
eqA |> println

   a^2*(-9*sqrt(2) + 9*sqrt(2)*sqrt(10 - 7*sqrt(2)) + 14*sqrt(10 - 7*sqrt(2)) + 20)^2/1156 - a*r5*(-9*sqrt(2) + 9*sqrt(20 - 14*sqrt(2)) + 14*sqrt(10 - 7*sqrt(2)) + 20)*(-3*sqrt(20 - 14*sqrt(2)) - 4*sqrt(10 - 7*sqrt(2)) + sqrt(-20*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11) + sqrt(2) + 2)/17 - 2*a*r5*(-5*sqrt(20 - 14*sqrt(2)) - 4*sqrt(10 - 7*sqrt(2)) + 4 + 5*sqrt(2))/17 + r5^2*(-3*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 4*sqrt(10 - 7*sqrt(2)) + sqrt(-20*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11) + sqrt(2) + 2)^2

res_r5 = solve(eqA, r5)[2]  # r5 決定
res_r5 |> println
res_r5(a => 1.5) |> N  # 0.13202643690561106

   0.13202643690561106

res_y5 = res_y5(r5 => res_r5) |> simplify  # y5 決定
res_y5 |> println
res_y5(a => 1.5) |> N  # 0.27493082244464034

   0.27493082244464034

6.　甲斜の長さを求める。

甲斜 = res_b^2 + a^2 |> expand |> simplify |> sqrt
甲斜 |> println
甲斜(a => 1.5) |> N  # 1.281304567672052

   sqrt(a^2*(-20*sqrt(20 - 14*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11))

   1.921956851508078

7.　6和を求める

(甲斜 + res_r0 + 2(res_r2 + res_r3 + res_r4 + res_r5))(a => 1.5) |> N  # 4.579089911176793

   4.579089911176793

和 = 甲斜 + res_r0 + 2(res_r2 + res_r3 + res_r4 + res_r5)
和 |> println

   a*(-40*sqrt(20 - 14*sqrt(2)) - 56*sqrt(10 - 7*sqrt(2)) - 6*sqrt(-34*sqrt(2) - 8*sqrt(2)*sqrt(10 - 7*sqrt(2)) + 52) - 8*sqrt(-17*sqrt(2) - 4*sqrt(2)*sqrt(10 - 7*sqrt(2)) + 26) + 2*sqrt(-40*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 56*sqrt(10 - 7*sqrt(2)) + 12*sqrt(2) + 22) + 4*sqrt(-20*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11) + 12*sqrt(2) + 21)*(-2*sqrt(-184*sqrt(2) + 14*sqrt(2)*sqrt(10 - 7*sqrt(2)) + 52*sqrt(10 - 7*sqrt(2)) + 14*sqrt(-20*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11) + 42*sqrt(2)*sqrt(10 - 7*sqrt(2))*sqrt(-20*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11) + 26*sqrt(2)*sqrt(-20*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11) + 156*sqrt(10 - 7*sqrt(2))*sqrt(-20*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11) + 390) - 9*sqrt(-40*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 56*sqrt(10 - 7*sqrt(2)) + 12*sqrt(2) + 22) - 2*sqrt(20 - 14*sqrt(2)) + 2*sqrt(2) + 12*sqrt(10 - 7*sqrt(2)) + 9*sqrt(-34*sqrt(2) - 8*sqrt(2)*sqrt(10 - 7*sqrt(2)) + 52) + 14*sqrt(-17*sqrt(2) - 4*sqrt(2)*sqrt(10 - 7*sqrt(2)) + 26) + 22 + 20*sqrt(-20*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11))/(17*(-40*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 56*sqrt(10 - 7*sqrt(2)) - 6*sqrt(2)*sqrt(10 - 7*sqrt(2))*sqrt(-20*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11) - 8*sqrt(10 - 7*sqrt(2))*sqrt(-20*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11) + 2*sqrt(2)*sqrt(-20*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11) + 4*sqrt(-20*sqrt(2)*sqrt(10 - 7*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11) + 12*sqrt(2) + 21)^2) + 2*a*(-23*sqrt(20 - 14*sqrt(2)) - 32*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 15)/17 + a*(-2 - sqrt(20 - 14*sqrt(2)) + 2*sqrt(2)) + a*(-1 + sqrt(2)) + a*(-5*sqrt(20 - 14*sqrt(2)) - 4*sqrt(10 - 7*sqrt(2)) + 4 + 5*sqrt(2))/17 + sqrt(a^2*(-20*sqrt(20 - 14*sqrt(2)) - 28*sqrt(10 - 7*sqrt(2)) + 6*sqrt(2) + 11))

6和を求める式は長いので，精一杯簡約化してもなお長い。

a = 1.5
v = 5√2 + 7
s = sqrt(10 - 7√2)
t = sqrt(11 + 6√2 - 4s*v)
u = sqrt(26 - √2(17 + 4s))
a*(2(2 + √2)t + 21 + 12√2 - 8v*s - 2(4 + 3√2)u)*
(-2√2sqrt((26 + 7√2)s + (7 + 13√2)t + (78 + 21√2)s*t + 195 - 92√2) + 2(6 - √2)s  + (20 - 9√2)t + (14 + 9√2)u + 2(11 + √2))/
(17(2(2 + √2)t - 8v*s - 2(4 + 3√2)s*t + 21 + 12√2)^2) +
a*(√2(4 - s) - 1 - (68 + 51√2)s/17 + sqrt(11 + 6√2 - 4v*s))

   4.579089911176797

正方形の一辺の長さが 1.5 のとき，6和は 4.579089911176797 である。

術では，「置二個開平方以減二個開平法加三個乗方面得六和」とあるが，そんなに短いわけがなく，適切な術でもない。

8.　数値解を求めるのは簡単である。

#=
using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (b, r0, r2, y2, r3, x3, r4, y4, r5, y5) = u
   return [
       a^2/2 - a*r0 - r0^2/2,  # eq1
       a^2/2 - a*r2 - a*y2 - r2^2/2 + r2*y2 + y2^2/2,  # eq2
       -r3^2/2 - r3*x3 + x3^2/2,  # eq3
       -r4^2/2 - r4*y4 + y4^2/2,  # eq4
       a^4 - 2*a^3*b + a^2*b^2 + 2*a^2*b*r0 - a^2*r0^2 - 2*a*b^2*r0,  # eq5
       -a^2*r2^2 + a^2*y2^2 - 2*a*b*r2*y2,  # eq6
       a^2*b^2 - 2*a^2*b*r3 - 2*a*b^2*x3 + 2*a*b*r3*x3 - b^2*r3^2 + b^2*x3^2,  # eq7
       a^2*b^2 - 2*a^2*b*y4 - a^2*r4^2 + a^2*y4^2 - 2*a*b^2*r4 + 2*a*b*r4*y4,  # eq8
       -a^2*r5^2 + a^2*y5^2 - 2*a*b*r5*y5,  # eq9
       -4*r2*r5 + y2^2 - 2*y2*y5 + y5^2,  # eq10
   ]
end;
a = 1.5
iniv = a .* BigFloat[0.801, 0.414, 0.222, 0.463, 0.19, 0.459, 0.178, 0.43, 0.088, 0.183]
res = nls(H, ini=iniv)
([1.2016314489305129, 0.6213203435596426, 0.33358494810779965, 0.694654694074625, 0.2850641966836687, 0.6882058497807045, 0.26723077635745685, 0.6451521645656638, 0.13202643690561106, 0.27493082244464034], true)
=#

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (b, r0, r2, y2, r3, x3, r4, y4, r5, y5) = [1.2016314489305129, 0.6213203435596426, 0.33358494810779965, 0.694654694074625, 0.2850641966836687, 0.6882058497807045, 0.26723077635745685, 0.6451521645656638, 0.13202643690561106, 0.27493082244464034]
   a = 1.5
   r1 = r0/2
   和 = sqrt(a^2 + b^2) + 2(r1 + r2 + r3 + r4 + r5)
   println("和 = $和")
   #(b, r0, r2, y2, r3, x3, r4, y4, r5) = [85.716, 44.321, 23.796, 49.552, 20.335, 49.092, 19.062, 46.021, 10]
   @printf("b = %g;  r0 = %g;  r2 = %g;  y2 = %g;  r3 = %g;  x3 = %g;  r4 = %g;  y4 = %g;  r5 = %g;  y5 = %g\n", b, r0, r2, y2, r3, x3, r4, y4, r5, y5)
   plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:blue, lw=0.5)
   circle(r0, a, r0, beginangle=180, endangle=360)
   circle(r0, a - r1, r1, :green)
   circle(a - r2, y2, r2, :magenta)
   circle(x3, r3, r3, :blue)
   circle(r4, y4, r4, :brown)
   circle(a - r5, y5, r5, :orange)
   segment(0, 0, a, a, :tomato)
   segment(0, b, a, 0, :tomato)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(0, a, "a ", :blue, :right, :vcenter)
       point(0, b, "b ", :tomato, :right, :vcenter)
       point(r0, a, "半円:r0,(r0,a)", :red, :center, :bottom, delta=delta/2)
       point(r0, a - r1, "乙円:r1,(r0,a-r1)", :green, :center, delta=-delta/2)
       point(a - r2, y2, "丙円:r2,(a-r2,y2)", :magenta, :center, delta=-delta/2)
       point(x3, r3, "丁円:r3,(x3,r3)", :blue, :center, delta=-delta/2)
       point(r4, y4, "戊円:r4,(r4,y4)", :brown, :center, delta=-delta/2)
       point(a - r5, y5, "己円:r5\n(a-r5,y5)", :black, :center, delta=-delta/2)
       plot!(xlims=a.*(-0.05, 1.05))
   end
end;

算額（その865）

岩手県平泉町　中尊寺阿弥陀堂（中尊寺地蔵院にて保管） 安政6年(1859)
http://www.wasan.jp/iwate/chusonji3.html

牧下英世：数学史を取り入れた授業実践―算額の教材化と総合的な学習―，2000筑波大学附属駒場論集第40集
https://tsukuba.repo.nii.ac.jp/record/6486/files/10.pdf

外円内に，水平な弦を 1 本と斜線を 2 本描き，区画された領域に大円 1 個と等円 3 個を入れる。外円と大円の直径がわかったとき，等円の直径はいかほどか。

弦と y 軸の交点座標を (0, y)
外円と斜線の交点を (x00, y00), (01, y01)
外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, r1 - R)
等円の半径と中心座標を r2, (0, R - r2), (x2, y + r2)
とおき，以下の連立方程式の数値解を求める。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, r2::positive,
     x2::positive, y::positive, x00::positive,
     y00::positice,  x01::positive, y01::positive, d
y = 2r1 - R
eq1 = dist(x01, y01, -x00, y00, x2, y + r2) - r2^2
eq2 = dist(-x01, y01, x00, y00, 0, R - r2) - r2^2
eq3 = dist(-x01, y01, x00, y00, 0, r1 - R) - r1^2
eq4 = x2^2 + (y + r2)^2 - (R - r2)^2
eq5 = (x01^2 + y01^2) - R^2
eq6 = (x00^2 + y00^2) - R^2
eq1 = numerator(apart(eq1, d)) |> simplify
eq2 = numerator(apart(eq2, d)) |> simplify
eq3 = numerator(apart(eq3, d)) |> simplify;

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (r2, x2, x00, y00, x01, y01) = u
   return [
R^2*x00^2 + 2*R^2*x00*x01 + R^2*x01^2 - 4*R*r1*x00^2 - 8*R*r1*x00*x01 - 4*R*r1*x01^2 - 2*R*r2*x00^2 - 4*R*r2*x00*x01 - 2*R*r2*x01^2 + 2*R*x00^2*y01 + 2*R*x00*x01*y00 + 2*R*x00*x01*y01 - 2*R*x00*x2*y00 + 2*R*x00*x2*y01 + 2*R*x01^2*y00 - 2*R*x01*x2*y00 + 2*R*x01*x2*y01 + 4*r1^2*x00^2 + 8*r1^2*x00*x01 + 4*r1^2*x01^2 + 4*r1*r2*x00^2 + 8*r1*r2*x00*x01 + 4*r1*r2*x01^2 - 4*r1*x00^2*y01 - 4*r1*x00*x01*y00 - 4*r1*x00*x01*y01 + 4*r1*x00*x2*y00 - 4*r1*x00*x2*y01 - 4*r1*x01^2*y00 + 4*r1*x01*x2*y00 - 4*r1*x01*x2*y01 - r2^2*y00^2 + 2*r2^2*y00*y01 - r2^2*y01^2 - 2*r2*x00^2*y01 - 2*r2*x00*x01*y00 - 2*r2*x00*x01*y01 + 2*r2*x00*x2*y00 - 2*r2*x00*x2*y01 - 2*r2*x01^2*y00 + 2*r2*x01*x2*y00 - 2*r2*x01*x2*y01 + x00^2*y01^2 + 2*x00*x01*y00*y01 - 2*x00*x2*y00*y01 + 2*x00*x2*y01^2 + x01^2*y00^2 - 2*x01*x2*y00^2 + 2*x01*x2*y00*y01 + x2^2*y00^2 - 2*x2^2*y00*y01 + x2^2*y01^2,  # eq1
R^2*x00^2 + 2*R^2*x00*x01 + R^2*x01^2 - 2*R*r2*x00^2 - 4*R*r2*x00*x01 - 2*R*r2*x01^2 - 2*R*x00^2*y01 - 2*R*x00*x01*y00 - 2*R*x00*x01*y01 - 2*R*x01^2*y00 - r2^2*y00^2 + 2*r2^2*y00*y01 - r2^2*y01^2 + 2*r2*x00^2*y01 + 2*r2*x00*x01*y00 + 2*r2*x00*x01*y01 + 2*r2*x01^2*y00 + x00^2*y01^2 + 2*x00*x01*y00*y01 + x01^2*y00^2,  # eq2
R^2*x00^2 + 2*R^2*x00*x01 + R^2*x01^2 - 2*R*r1*x00^2 - 4*R*r1*x00*x01 - 2*R*r1*x01^2 + 2*R*x00^2*y01 + 2*R*x00*x01*y00 + 2*R*x00*x01*y01 + 2*R*x01^2*y00 - r1^2*y00^2 + 2*r1^2*y00*y01 - r1^2*y01^2 - 2*r1*x00^2*y01 - 2*r1*x00*x01*y00 - 2*r1*x00*x01*y01 - 2*r1*x01^2*y00 + x00^2*y01^2 + 2*x00*x01*y00*y01 + x01^2*y00^2,  # eq3
x2^2 - (R - r2)^2 + (-R + 2*r1 + r2)^2,  # eq4
-R^2 + x01^2 + y01^2,  # eq5
-R^2 + x00^2 + y00^2,  # eq6
   ]
end;
R = 10
r1 = 7
iniv = R .* BigFloat[0.24326219426446974, 0.5286032540384469, 0.9666966139569063, -0.2559250995198634, 0.5325907580969444, 0.8463728991347266]
res = nls(H, ini=iniv)

   ([2.1106684356050365, 4.9901186161311815, 9.935099850667232, -1.137449320748823, 5.01652946256841, 8.65068969222588], true)

外円の直径が 20，大円の直径が 14 のとき，等円の直径は 4.221336871210073 である。

その他のパラメータは以下のとおりである。

   R = 10;  r1 = 7;  y = 4;  r2 = 2.11067;  x2 = 4.99012;  x00 = 9.9351;  y00 = -1.13745;  x01 = 5.01653;  y01 = 8.65069

算額に書かれている術は次のとおりである。注
術曰置外圓径大圓径以除之開平方加一個以除外圓径二段内滅大圓径除得等圓径合問

現代文で書くと，以下のようになろう。
外円の直径を大円の直径で割り，この平方根を求め，1 を加えたもので，外円の直径を 2 倍したものを割り，大円の直径を引くと等円の直径が得られる，これは問に合っている。

式で書くと，外円，大円の直径をそれぞれ「外」，「大」とすれば，2外/(sqrt(外/大) + 1) - 大 で，外円の直径が 20，大円の直径が 14 のとき，等円の直径が 4.22133687121007 であるとわかる。
これは，上に述べた数値解と一致する。

注：牧下は術の前半 17 文字を抜いてるので，意味をなさなくなっている。wasan.jp の算額の写真は不鮮明であるがここに書いたものと相違ない（数値解と一致するので間違いない）。

外 = 20
大 = 14
2外/(sqrt(外/大) + 1) - 大 |> println

   4.22133687121007

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   # R = 1
   # r1 = 0.65
   y = 2r1 - R
   (r2, x2, x00, y00, x01, y01) = [28, 60, 110, -32, 60, 97]
   (r2, x2, x00, y00, x01, y01) = res[1]
   println("外円の直径が $(2R)，大円の直径が $(2r1) のとき，等円の直径は $(2r2) である。")
   @printf("R = %g;  r1 = %g;  y = %g;  r2 = %g;  x2 = %g;  x00 = %g;  y00 = %g;  x01 = %g;  y01 = %g\n", R, r1, y, r2, x2, x00, y00, x01, y01)
   plot()
   circle(0, 0, R)
   circle(0, r1 - R, r1, :blue)
   circle(0, R - r2, r2, :green)
   circle2(x2, y + r2, r2, :green)
   x0 = sqrt(R^2 - y^2)
   segment(-x0, y, x0, y, :magenta)
   segment(-x01, y01, x00, y00)
   segment(x01, y01, -x00, y00)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R - r2, "等円:r2\n(0,R-r2)", :green, :center, delta=-delta/2)
       point(x2, y + r2, "等円:r2\n(x2,y+r2)", :green, :center, delta=-delta/2)
       point(0, r1 - R, "大円:r1\n(0,r1-R)", :blue, :center, delta=-delta/2)
       point(x00, y00, "(x00,y00)", :red, :right, delta=-delta/2, deltax=-delta/2)
       point(x01, y01, "(x01,y01)", :red, :left, :bottom, delta=delta/2)
   end
end;

算額（その864）

岩手県平泉町　中尊寺阿弥陀堂（中尊寺地蔵院にて保管） 安政6年(1859)
http://www.wasan.jp/iwate/chusonji3.html

牧下英世：数学史を取り入れた授業実践―算額の教材化と総合的な学習―，2000筑波大学附属駒場論集第40集
https://tsukuba.repo.nii.ac.jp/record/6486/files/10.pdf

正方形内に正三角形と斜線，甲円と乙円が入っている。甲円と乙円の直径の差がわかっているとき，正方形の一辺の長さを求めよ。

正方形の一辺の長さを 2a
甲円の半径と中心座標を r1, (2a - r1, y1)
乙円の半径と中心座標を r2, (r2, y2); r1 > r2
直径の差を K; r1 = r2 + K/2
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, r1::positive, y1::positive,
     r2::positive, y2::positive, K::positive, d
s3 = √Sym(3)
r1 = r2 + K/2
eq1 = dist(2a, 0, a, s3*a, 2a - r1, y1) - r1^2
eq2 = dist(0, 0, a, s3*a, r2, y2) - r2^2
eq3 = dist(2a, 2a, a, s3*a, 2a - r1, y1) - r1^2
eq4 = dist(2a, 2a, a, s3*a, r2, y2) - r2^2
eq1 = numerator(apart(eq1, d)) |> simplify
eq2 = numerator(apart(eq2, d)) |> simplify
eq3 = numerator(apart(eq3, d)) |> simplify
eq4 = numerator(apart(eq4, d)) |> simplify;
# res = solve([eq1, eq2, eq3, eq4], (a, y1, r2, y2))

println(eq1, ",  # eq1")
println(eq2, ",  # eq2")
println(eq3, ",  # eq3")
println(eq4, ",  # eq4")

   -K^2/16 - K*r2/4 - sqrt(3)*K*y1/4 - r2^2/4 - sqrt(3)*r2*y1/2 + y1^2/4,  # eq1
   -r2^2/4 - sqrt(3)*r2*y2/2 + y2^2/4,  # eq2
   -K^2/8 - sqrt(3)*K^2/16 - K*a/2 - K*r2/2 - sqrt(3)*K*r2/4 + K*y1/4 + sqrt(3)*a^2 + 2*a^2 - a*r2 - 2*a*y1 - sqrt(3)*a*y1 - r2^2/2 - sqrt(3)*r2^2/4 + r2*y1/2 + sqrt(3)*y1^2/4 + y1^2/2,  # eq3
   2*a^2 - a*r2 + sqrt(3)*a*r2 - sqrt(3)*a*y2 - a*y2 - r2^2/2 - sqrt(3)*r2^2/4 - r2*y2/2 + sqrt(3)*y2^2/4 + y2^2/2,  # eq4

eq2, eq1 を解いて，r2, y1 を求める。

res1 = solve(eq2, r2)[1]  # r2
res1 |> println

   y2*(2 - sqrt(3))

res2 = solve(eq1, y1)[2] |> factor # y1 2番目が適解
res2 |> println

   (sqrt(3) + 2)*(K + 2*r2)/2

eq3, eq4 に r2, y1 を代入して，変数消去する。

eq13 = eq3(y1 => res2, r2 => res1) |> simplify
eq13 |> println

   sqrt(3)*K^2 + 7*K^2/4 - 4*K*a - 2*sqrt(3)*K*a + sqrt(3)*K*y2 + 2*K*y2 + sqrt(3)*a^2 + 2*a^2 - 4*a*y2 + y2^2

eq14 = eq4(y1 => res2, r2 => res1) |> simplify
eq14 |> println

   2*a^2 - 6*a*y2 + 2*sqrt(3)*a*y2 - y2^2 + sqrt(3)*y2^2

eq14 から y2 を求めて，それを eq13 に代入して変数消去する。

res3 = solve(eq14, y2)[2] |> simplify # y2 2番目が適解
res3 |> println

   a*(-sqrt(42 - 24*sqrt(3)) - sqrt(14 - 8*sqrt(3)) + 2*sqrt(3))/2

eq23 = eq13(y2 => res3) |> simplify
eq23 |> println

   sqrt(3)*K^2 + 7*K^2/4 - K*a - 3*K*a*sqrt(42 - 24*sqrt(3))/2 - 5*K*a*sqrt(14 - 8*sqrt(3))/2 - 4*sqrt(3)*a^2 - a^2*sqrt(14 - 8*sqrt(3)) + a^2*sqrt(42 - 24*sqrt(3)) + 7*a^2

eq23 を a について求める。K だけを含む式になる。

res99 = solve(eq23, a)[1] |> simplify  # a 1番目が適解
res99 |> println

   K*(5*sqrt(14 - 8*sqrt(3)) + 3*sqrt(42 - 24*sqrt(3)) + 2 + 2*sqrt(sqrt(3) + 2))/(4*(-4*sqrt(3) - sqrt(2)*sqrt(7 - 4*sqrt(3)) + sqrt(6)*sqrt(7 - 4*sqrt(3)) + 7))

res99 には K が含まれているので simplify できないが，K にかかる係数は単に数値演算なので，簡約化できる。a = K*(4√3 + 7)/2 である。

@syms d
res999 = apart(res99/K, d)*K |> simplify  # a
res999 |> println

   K*(4*sqrt(3) + 7)/2

K に具体的な数値を代入すれば a の値が求まる。

res_a = res999(K => 5042).evalf()  # a
res_a |> println

   35113.0003435246

この後，逆順に代入していくことにより各変数の値を求めることができる。

res_y2 = res3(K => 5042, a => res_a).evalf()  # y2
res_y2 |> println

   42641.6741619770

res_r2 = res1(K => 5042, y2 => res_y2).evalf()  # r2
res_r2 |> println

   11425.8021556128

res_y1 = res2(K => 5042, r2 => res_r2).evalf()  # y1
res_y1 |> println

   52050.1742478581

甲円と乙円の直径の差が 5042 のとき，正方形の一辺の長さは 35113.0003435246 である。

その他のパラメータは以下のとおりである。
K = 5042; a = 35113;  r1 = 13946.802;  y1 = 52050.174;  r2 = 11425.802;  y2 = 42641.674

以下により，一挙に数値解を求めることもできる。

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (a, y1, r2, y2) = u
   return [
       -(K/2 + r2)^2 + (y1 - sqrt(3)*(sqrt(3)*a*y1 - a*(-K/2 - r2))/(4*a))^2 + (-K/2 - r2 - (-sqrt(3)*a*y1/2 + a*(-K/2 - r2)/2)/(2*a))^2,  # eq1
       -r2^2 + (r2 - (a*r2/2 + sqrt(3)*a*y2/2)/(2*a))^2 + (y2 - sqrt(3)*(a*r2 + sqrt(3)*a*y2)/(4*a))^2,  # eq2
       -(K/2 + r2)^2 + (-K/2 + a*(-a*(-K/2 - r2) + (-2*a + y1)*(-2*a + sqrt(3)*a))/(a^2 + (-2*a + sqrt(3)*a)^2) - r2)^2 + (-2*a + y1 - (-2*a + sqrt(3)*a)*(-a*(-K/2 - r2) + (-2*a + y1)*(-2*a + sqrt(3)*a))/(a^2 + (-2*a + sqrt(3)*a)^2))^2,  # eq3
       -r2^2 + (-2*a + y2 - (-2*a + sqrt(3)*a)*(-a*(-2*a + r2) + (-2*a + y2)*(-2*a + sqrt(3)*a))/(a^2 + (-2*a + sqrt(3)*a)^2))^2 + (-2*a + a*(-a*(-2*a + r2) + (-2*a + y2)*(-2*a + sqrt(3)*a))/(a^2 + (-2*a + sqrt(3)*a)^2) + r2)^2,  # eq4
   ]
end;
K = 5042
iniv = BigFloat[35, 52, 11, 42].*1000
res = nls(H, ini=iniv)

   ([35113.000343524545, 52050.17424785807, 11425.802155612791, 42641.67416197693], true)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   s3 = √3
   K = 5042
   a = K*(4s3 + 7)/2
   y2 = a*(2s3 - sqrt(42 - 24s3) - sqrt(14 - 8s3))/2
   r2 = y2*(2 - s3)
   y1 = (s3 + 2)*(K + 2*r2)/2
   r1 = r2 + K/2
   @printf("K = %.8g; a = %.8g;  r1 = %.8g;  y1 = %.8g;  r2 = %.8g;  y2 = %.8g\n", K, a, r1, y1, r2, y2)
   plot([0, 2a, 2a, 0, 0], [0, 0, 2a, 2a, 0], color=:black, lw=0.5)
   plot!([0, 2a, a, 0], [0, 0, √3a, 0], color=:green, lw=0.5)
   circle(2a - r1, y1, r1)
   circle(r2, y2, r2, :blue)
   segment(0, 2a - 2(2a - √3a), 2a, 2a, :magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(2a - r1, y1, "甲円:r1,(2a-r1,y1)", :red, :center, delta=-delta/2)
       point(r2, y2, "乙円:r2,(r2,y2)", :blue, :center, delta=-delta/2)
       point(a, √3a, "(a,√3a)", :green, :right, :bottom, delta=delta/2)
       point(a, 0, " a", :black, :left, :bottom, delta=delta/2)
       point(2a, 0, " 2a", :black, :left, :bottom, delta=delta/2)
       plot!(xlims=(0, 75000))
   end
end;

算額（その863）

三十三　岩手県一関市舞川相川 菅原神社 嘉永3年(1850)

山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

正方形内に四分円 2 個，半円 1 個，大円 1 個，小円 1 個を入れる。小円の直径が 17 寸のとき，大円の直径はいかほどか。

四分円の半径と中心座標を r0, (0, 0), (r0, r0)
半円の半径と中心座標を r0/2, (0, r0/2)
大円の半径と中心座標を r1, (x1, r0 - x1)
小円の半径と中心座標を r2, (x2, y2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms r0::positive, r1::positive, x1::positive,
     r2::positive, x2::positive, y2::positive
eq1 = (r0 - x2)^2 + (r0/2 - y2)^2 - (r2 + r0/2)^2
eq2 = (r0 - x1)^2 + (r0 - x1 - r0/2)^2 - (r1 + r0/2)^2
eq3 = (r0 - x2)^2 + (r0 - y2)^2 - (r0 - r2)^2
eq4 = x1^2 + (r0 - x1)^2 - (r0 - r1)^2
eq5 = (x2 - x1)^2 + (r0 - x1 - y2)^2 - (r1 + r2)^2
res = solve([eq1, eq2, eq3, eq4, eq5], (r0, r1, x1, x2, y2))

   2-element Vector{NTuple{5, Sym{PyCall.PyObject}}}:
    (9*r2/4, 9*r2/17, 45*r2/68, 5*r2/4, 3*r2)
    (33*r2/4, 33*r2/17, 165*r2/68, 13*r2/4, 3*r2)

2 組の解が得られるが，2 番目のものが適解である。

大円の半径は小円の半径の 33/17 倍である。
すなわち，小円の直径が 17 寸のとき，大円の直径は 33 寸である。

その他のパラメータは以下のとおりである。
r2 = 8.5;  r0 = 70.125;  r1 = 16.5;  x1 = 20.625;  x2 = 27.625;  y2 = 25.5

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 17/2
   (r0, r1, x1, x2, y2) = r2 .* (33/4, 33/17, 165/68, 13/4, 3)
   @printf("小円の直径が %g のとき，大円の直径は %g\n", 2r2, 2r1)
   @printf("r2 = %g;  r0 = %g;  r1 = %g;  x1 = %g;  x2 = %g;  y2 = %g\n", r2, r0, r1, x1, x2, y2)
   plot([0, r0, r0, 0, 0], [0, 0, r0, r0, 0], color=:black, lw=0.5)
   circle(0, 0, r0, beginangle=0, endangle=90)
   circle(r0, r0, r0, beginangle=180, endangle=270)
   circle(r0, r0/2, r0/2, :magenta, beginangle=90, endangle=270)
   circle(x1, r0 - x1, r1, :green)
   circle(x2, y2, r2, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r0, 0, " r0", :black, :left, :bottom, delta=delta/2)
       point(0, r0, " r0", :black, :left, :bottom, delta=delta/2)
       point(r0, r0/2, "(r0,r0/2)", :black, :right, :bottom, delta=delta)
       point(x1, r0 - x1, "大円:r1,(x1,r0-x1)", :green, :center, delta=-delta/2)
       point(x2, y2, "小円:r2,(x2,y2)", :orange, :center, delta=-delta/2)
   end
end;

算額（その862）

二十六　岩手県一関市萩荘 赤萩観音寺前額

山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

全円内に大円 1 個，中円 2 個，小円 4 個と菱形が入っている。小円の直径を知って，全円の直径を求めよ。注：「中円 4 個，小円 2 個」と書いているが明らかに誤記であろう。

大円の直径は小円の直径の (1 + √2) 倍である。これを踏まえると，大円と中円と菱形が全円の中に入っているとき，全円の直径を求めよという問題になる。それは，算額（その445）https://blog.goo.ne.jp/r-de-r/e/9f35b3c1b37302b50c61355f43956949 と同じ問題であるが，そこに示したように，描画パラメータは 5 個で，既知のパラメータはそのうちの 2 個，条件は 3 つなので，方程式は解くことができる。しかし，本問では既知の条件は1つしかないので，方程式は解けない。方程式を解くためには既知のパラメータをもう 1 つ見つける必要がある。とはいっても，もっとも単純に「大円の直径が全円の半径に等しい」と仮定する以外の妥当な方策はない。

大円の直径は小円の直径の (1 + √2) 倍なので，全円の直径は小円の直径の 2(1 + √2) ≒ 4.82842712474619 倍である。

術では「全円の直径は小円の直径の 5 倍」としているが，疑問である。

算額の答えはここまでである。

以下では，図を描くために，中円のパラメータを求める。

全円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, R - r1)
中円の半径と中心座標を r2, (x2, y2)
小円の半径と中心座標を r3, (r1 - r3, R - r1)
とおき，以下の連立方程式を解く。

パラメータは以下のとおりである。

   r3 = 0.5;  r1 = 1.20711;  R = 2.41421;  r2 = 0.804738;  x2 = 1.60948;  y2 = 0

include("julia-source.txt");

using SymPy
@syms b::positive, R::positive, r1::positive,
     r2::positive, x2::positive, y2,
     r3::positive, d
r3 = 1//2
r1 = (1 + √Sym(2))r3
R = 2r1
b = R - r1
eq1 = x2^2 + y2^2 - (R - r2)^2
eq2 = x2^2 + (R - r1 - y2)^2 - (r1 + r2)^2
eq3 = dist(0, 0, sqrt(R^2 - (b - R)^2), b - R, x2, y2) - r2^2
# eq4 = 2(r1 - r3)^2 - 4r3^2
res = solve([eq1, eq2, eq3], (r2, x2, y2))

   1-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (1/3 + sqrt(2)/3, sqrt(8*sqrt(2)/9 + 4/3), 0)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r3 = 1/2
   r1 = (1 + √2)r3
   R = 2r1
   (r2, x2, y2) = (1/3 + sqrt(2)/3, sqrt(8*sqrt(2)/9 + 4/3), 0)
   @printf("r3 = %g;  r1 = %g;  R = %g;  r2 = %g;  x2 = %g;  y2 = %g\n", r3, r1, R, r2, x2, y2)
   b = R - r1
   plot()
   circle(0, 0, R, :green)
   circle(0, R - r1, r1)
   circle2(r1 - r3, R - r1, r3, :magenta)
   circle(0, R - r3, r3, :magenta)
   circle(0, R - 2r1 + r3, r3, :magenta)
   circle(x2, y2, r2, :blue)
   x = sqrt(R^2 - (b - R)^2)
   plot!([0, x, 0, -x, 0], [-R, b - R, 2b -R, b - R, -R], color=:orange, lw=0.5)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(R, 0, " R", :green, :left, :bottom, delta=delta/2)
       point(0, R - r1, "大円:r1,(0,R-r1)", :red, :center, delta=-delta)
       point(x2, y2, "中円:r2\n(x2,y2)", :blue, :center, delta=-delta/2)
       point(r1 - r3, R - r1, "小円:r3\n(r1-r3,R-r1)", :magenta, :center, :bottom, delta=delta)
       point(0, b - R, " b", :orange, :left, :vcenter)
   end
end;

算額（その861）

二十四　岩手県一関市萩荘字八幡 達古袋八幡神社 弘化3年

山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

大円の一部である円弧内に正三角形2個と小円が入っている。正三角形の一辺の長さと小円の直径がわかっているときに大円の直径を求める術は如何に。

問では，「正三角形の一辺の長さと小円の直径がわかっているときに」とあるが，一般的にこの2つを任意に指定すると，図形を構成することは不可能である。正三角形の一辺の長さ，小円の直径，大円の直径の 3 変数のうち，1 つだけを指定して残りの 2 つのパラメータを決定するというのが妥当であろう。

よって，以下のように定めて連立方程式を解く。
大円の半径と中心座標を R, (0, 0)
小円の半径と中心座標を r, (0, R -r)
正三角形の一辺の長さを a とする。

eq1 は小円の中心と正三角形の一辺までの距離が小円の半径に等しいこと，
eq2 は正三角形の頂点が大円の円周上にあることを意味している。

include("julia-source.txt");

using SymPy
@syms R::positive, r::positive, a::positive, x::positive
x = sqrt(R^2 - (R - 2r)^2)
eq1 = dist(x - a, R - 2r, x - a/2, R - 2r + a√Sym(3)/2, 0, R - r) - r^2
eq2 = (x - a/2)^2 + (R - 2r + a√Sym(3)/2)^2 - R^2
res = solve([eq1, eq2], (R, a));

2 組の解が得られるが，2 番目のものが適解である。

大円の半径は，小円の半径の 7/3，正三角形の一辺の長さは小円の半径の √3 倍である。

「術」は不適切である。

res[2]

   (7*r/3, sqrt(3)*r)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1//2
   (R, a) = (7*r/3, sqrt(3)*r)
   x = sqrt(R^2 - (R - 2r)^2)
   plot()
   circle(0, 0, R, :green)
   circle(0, R - r, r)
   plot!([x - a, x - a/2, x], R - 2r .+ [0, √3a/2, 0], color=:blue, lw=0.5)
   plot!(-[x - a, x - a/2, x], R - 2r .+ [0, √3a/2, 0], color=:blue, lw=0.5)
   segment(-x, R - 2r, x, R - 2r, :black)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(R, 0, " R", :green, :left, :bottom, delta=delta/2)
       point(0, R, " R", :green, :left, :bottom, delta=delta/2)
       point(0, R - 2r, "R-2r", :black, :center, delta=-delta/2)
       point(0, R - r, " R-r", :red, :left, :vcenter)
       point(sqrt(R^2 - (R - 2r)^2), R - 2r, "(√(R^2-(R-2r)^2),R-2r)", :black, :right, delta=-delta/2)
   end
end;

算額（その860）

二十四　岩手県一関市萩荘字八幡 達古袋八幡神社 弘化3年

山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

水平線の上に菱形と小円 3 個を内接する大円とそれ左側にあり大円と外接する小円がある。小円の直径が 1 寸のとき，左側の小円と大円と直線に挟まれる面積（黒積）を求めよ。

大円とそれに内接する小円 3 個，菱形 1 個は，算額（その851）にあるとおりで，小円の直径を r とすると，大円の直径は 3r である。

include("julia-source.txt");

using SymPy
@syms R::positive, r::positive, x::positive, y::positive,
   x2::negative
y = r
eq1 = x^2 + y^2 - (R - r)^2
eq2 = x^2 + (R - r - y)^2 - 4r^2
eq3 = x2^2 + (r - R)^2 - (R + r)^2　
res = solve([eq1, eq2, eq3], (R, x, x2))[1]

   (3*r, sqrt(3)*r, -2*sqrt(3)*r)

小円，大円と直線により区分される面積は，台形の面積から小円の面積の 1/3 と大円の面積の 1/6 を引いたものである。
S = 2√3*r - 11π*r^2/6

@syms r, R
R = 3r
s3 = √Sym(3)
S = (r + R)*s3(R - r)/2 - PI*r^2/3 - PI*R^2/6
S |> println

   -11*pi*r^2/6 + 2*sqrt(3)*r

r = 1/2 のとき，S = 0.2921541746735554 である。

S(r => 1/2) |> N

   0.2921541746735554

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1/2
   (R, x, x2) = r .* (3, √3, -2√3)
   y = r
   b = R - r
   y0 = -r
   x0 = sqrt(R^2 - y0^2)
   plot([x2, 0, 0, x2, x2], [-R, -R, 0, r - R, -R], seriestype=:shape, fillcolor=:gray30)
   circlef(0, 0, R, :orange)
   circlef(0, R - r, r, :cyan)
   circlef(x, y, r, :cyan)
   circlef(-x, y, r, :cyan)
   plot!([x0, 0, -x0, 0, x0], [-r, R - 2r, -r, -R, b - R], color=:red, seriestype=:shape, lw=0.5, alpha=0.5)
   circlef(x2, r - R, r, :cyan)
   segment(x2, -R, 0, -R, :cyan)
   plot!([x2, 0, 0, x2, x2], [-R, -R, 0, r - R, -R], color=:black, lw=1)
   circle(0, 0, 0.2, :black, beginangle=210, endangle=270)
   circle(x2, r - R, 0.2, :black, beginangle=270, endangle=390)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R, " R", :red, :center, :bottom, delta=delta/2)
       point(R, 0, " R", :red, :left, :vcenter)
       point(0, R - r, "小円:r,(0,R-r)", :green, :center, delta=-delta/2)
       point(x, r, "小円:r,(x,r)", :green, :center, delta=-delta/2)
       point(x2, r - R, "小円:r \n(x2,r-R) ", :green, :right, :vcenter)
       point(0, -r, " -r", :white, :left, :vcenter)
       point(2√2r, -r, "(2√2r,-r)  ", :white, :right, :vcenter)
       point(0, -0.25, "60°", :black, :right, mark=false)
       point(x2 + 0.2, r - R, "120°", :black, :left, mark=false)
   end
end;

算額（その859）

二十四　岩手県一関市萩荘字八幡 達古袋八幡神社 弘化3年

山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

長方形内に大円が内接する不等辺三角形を入れ，大きさの同じ小円を左側に複数個，右側に 1 個入れる。小円の直径がわかっているとき，左側の小円の個数と大円の直径を求めよ。

なお，前もって述べるが，術では「(左側の小円の個数÷2 + 1)×小円径=大円径」とあるが，この式は一般には成り立たない。

また，左側の小円の個数が 1 個の場合は「算額（その857）」と同じになるが，その場合も，算額（その857）で述べた通り，示された条件だけでは不足であり，たとえば長方形の長辺の長さが既知でなければ一意な解はない。さらに，左側の小円の個数も未知として方程式を解くことは適切とは思えない。小円の個数も与えたうえで大円の直径を求めよとするのが妥当であろう。

長方形の長辺と短辺の長さを a, b
不等辺三角形の頂点の座標を (c, b)
大円の半径と中心座標を r1, (x1, r1)
小円の半径と中心座標を r2, (r2, b - (2n - 1)*r2), (a - r2, b - r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms a::positive, b::positive, c::positive, n::integer,
     r1::positive, x1::positive, r2::positive, d
l1 = sqrt(b^2 + c^2)
l2 = sqrt(b^2 + (a - c)^2)
S1 = (a + l1 + l2)*r1/2
S2 = (b + c*(2n - 1) + l1)*r2/2
S3 = ((a - c) + b + l2)*r2/2
eq1 = (S2 + S3) - S1
eq2 = numerator(apart(dist(0, 0, c, b, x1, r1) - r1^2, d))
eq3 = numerator(apart(dist(c, b, a, 0, x1, r1) - r1^2, d))
eq4 = numerator(apart(dist(c, b, a, 0, a - r2, b - r2) - r2^2, d))
eq5 = (a - c) + b - l2 - 2r2;

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (b, c, r1, x1) = u
   return [
       -r1*(a + sqrt(b^2 + c^2) + sqrt(b^2 + (a - c)^2))/2 + r2*(b + c*(2*n - 1) + sqrt(b^2 + c^2))/2 + r2*(a + b - c + sqrt(b^2 + (a - c)^2))/2,  # eq1
       -b^2*r1^2 + b^2*x1^2 - 2*b*c*r1*x1,  # eq2
       a^2*b^2 - 2*a^2*b*r1 - 2*a*b^2*x1 + 2*a*b*c*r1 + 2*a*b*r1*x1 - b^2*r1^2 + b^2*x1^2 - 2*b*c*r1*x1,  # eq3
       a + b - c - 2*r2 - sqrt(b^2 + (a - c)^2),  # eq5
   ]
end;

左側の小円が 1 個の場合に，算額（その857）と同じになる。
算額（その857）は大円の直径から小円の直径を求めるものであるが，長方形の長辺が 2，大円の直径が 1 のとき，小円の直径が 2/3 である。
本算額では，以下のように小円の直径から大円の直径を求めることになる。

a = 2
n = 1
r2 = 1/3
iniv = BigFloat[2, 1.5, 0.6, 1.2]
res = nls(H, ini=iniv)

   ([1.3333333333333333, 1.0, 0.49999999999999994, 1.0], true)

長方形の長辺が 2，小円の直径が 2/3，個数が 1 のとき，大円の直径は 1 である。

「術」の「(左側の小円の個数÷2 + 1)×小円径=大円径」は一般には成り立たない。

a = 4;  b = 1.5;  c = 2;  n = 1;  r1 = 0.666667;  x1 = 2
小円の直径が 1，個数が 1，長方形の長辺が 4 のとき，大円の直径は 1.33333 である。
術による大円の直径 = 1.5

a = 4;  b = 2.70711;  c = 2.70711;  n = 2;  r1 = 1;  x1 = 2.41421
小円の直径が 1，個数が 2，長方形の長辺が 4 のとき，大円の直径は 2 である。
術による大円の直径 = 2

a = 4;  b = 4.10074;  c = 2.83875;  n = 3;  r1 = 1.23801;  x1 = 2.36272
小円の直径が 1，個数が 3，長方形の長辺が 4 のとき，大円の直径は 2.47602 である。
術による大円の直径 = 2.5

a = 4;  b = 5.53944;  c = 2.88985;  n = 4;  r1 = 1.39379;  x1 = 2.29917
小円の直径が 1，個数が 4，長方形の長辺が 4 のとき，大円の直径は 2.78757 である。
術による大円の直径 = 3

a = 4;  b = 7;  c = 2.91667;  n = 5;  r1 = 1.5;  x1 = 2.25
小円の直径が 1，個数が 5，長方形の長辺が 4 のとき，大円の直径は 3 である。
術による大円の直径 = 3.5

a = 20;  b = 15.5568;  c = 18.9657;  n = 15;  r1 = 5.17517;  x1 = 14.4693
小円の直径が 1，個数が 15，長方形の長辺が 20 のとき，大円の直径は 10.3503 である。
術による大円の直径 = 8.5

a = 20
n = 15
r2 = 1/2
iniv = BigFloat[2, 1.5, 0.6, 1.2].*10
res = nls(H, ini=iniv)
function draw(more=false)
   pyplot(size=(500, 500), showaxis=true, grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (b, c, r1, x1) = res[1]
   str = @sprintf("2r2=%g, n=%g, a=%g\n --> 2r1=%g", 2r2, n, a, 2r1)
   @printf("a = %g;  b = %g;  c = %g;  n = %g;  r1 = %g;  x1 = %g\n", a, b, c, n, r1, x1)
   @printf("小円の直径が %g，個数が %g，長方形の長辺が %g のとき，大円の直径は %g である。\n", 2r2, n, a, 2r1)
   @printf("術による大円の直径 = %g\n", (n/2 + 1)*2r2)
   plot([0, a, a, 0, 0], [0, 0, b, b, 0], color=:blue, lw=0.5)
   circle(x1, r1, r1)
   circle(a - r2, b - r2, r2, :green)
   for i = 1:n
       circle(r2, b - (2i - 1)*r2, r2, :orange)
   end
   plot!([0, c, a], [0, b, 0], color=:magenta, lw=0.5)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x1, 0.1r1, str, :black, :center, :bottom, delta=delta/2, mark=false)
       point(x1, r1, "大円:r1,(x1,r1)", :red, :center, delta=-delta/2)
       point(r2, b - (2n - 1)r2, "小円:r2,(r2,b-(2n-1)r2)", :black, :left, :bottom, delta=delta/2)
       point(a - r2, b - r2,"小円:r2,(a-r2,b-r2)", :black, :right, delta=-delta/2)
   end
end;