2018-08-01

ESL2章

ESL

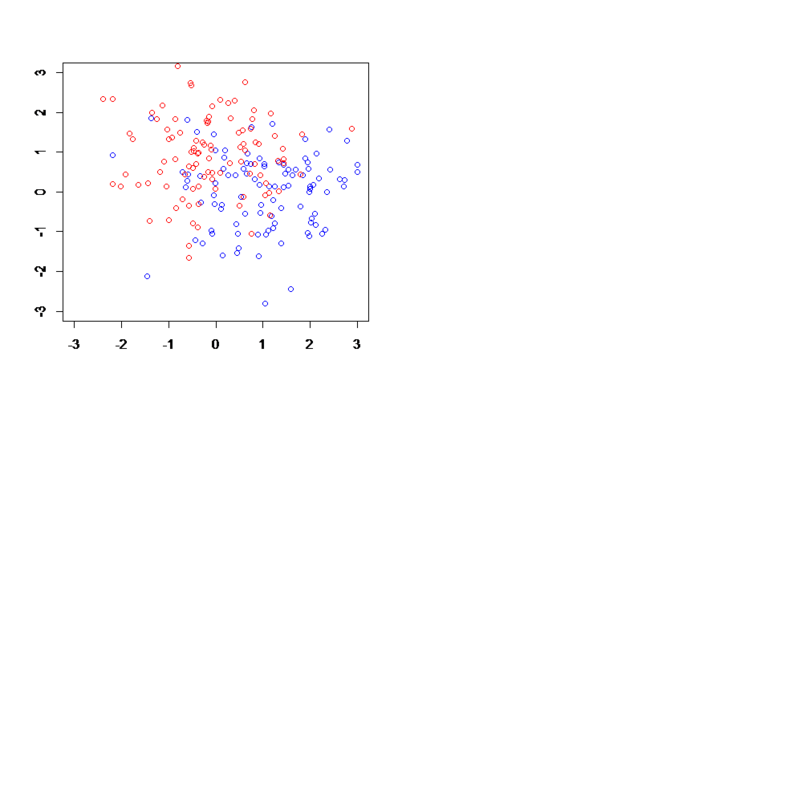
figure 2.4について

library(MASS)
blue_ave<-c(1,0)
red_ave<-c(0,1)
blue<-mvrnorm(100,blue_ave,diag(2))
red<-mvrnorm(100,red_ave,diag(2))
cl<-factor(c(rep("blue",100),rep("red",100)))
train<-rbind(blue,red)
test<-rbind(mvrnorm(5000,blue_ave,diag(2)/5),mvrnorm(5000,red_ave,diag(2))/5)

test_answer<-c(rep("blue",5000),rep("red",5000))
test_error<-c()
for (i in 1:200){
classres <- knn(train,test,cl,k=i,prob=T)
test_error<-c(test_error,length(which(classres==test_answer)))
}
plot(1-test_error/10000)

train_answer<-c(rep("blue",100),rep("red",100))
train_error<-c()
for (i in 1:200){
classres <- knn(train,train,cl,k=i,prob=T)
train_error<-c(train_error,length(which(classres==train_answer)))
}
plot(1-train_error/200)

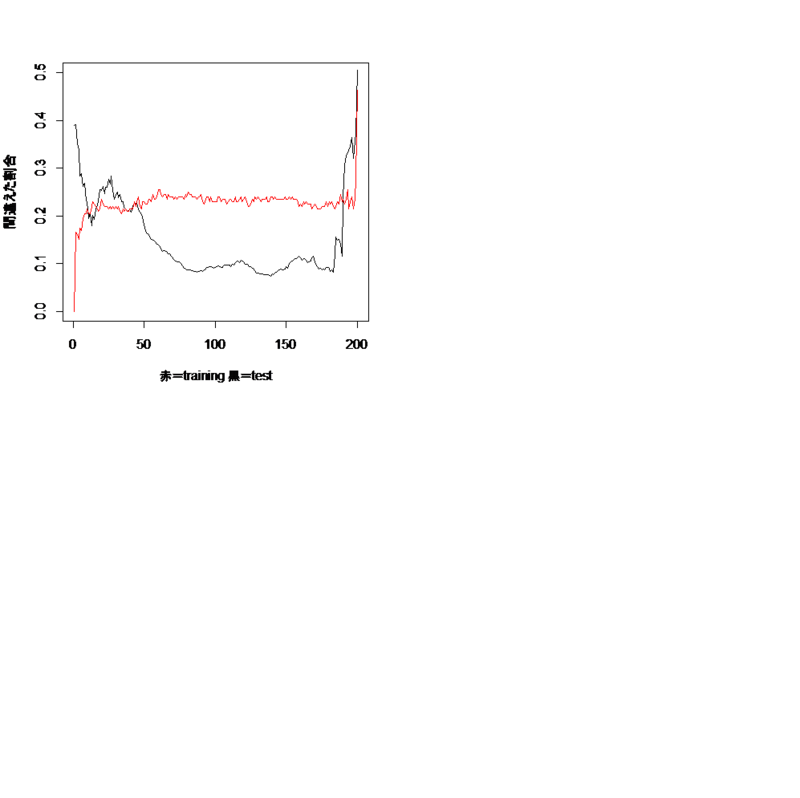
plot(1-test_error/10000,type="l",ylim=c(0,0.5),xlab="",ylab="")
par(new=T)
plot(1-train_error/200,col="red",type="l",ylim=c(0,0.5),xlab="赤＝training 黒＝test",ylab="間違えた割合")

plot(blue,col="blue",xlim=c(-3,3),ylim=c(-3,3),xlab="",ylab="")
par(new=T)
plot(red,col="red",xlim=c(-3,3),ylim=c(-3,3),xlab="",ylab="")

2018-05-27

ルードヴィッヒモデル

数理モデル

検索してもあまりいいページ出てこなかったですが式は以下の通り
$\dot{n}=rn(1-\frac{n}{k})-\frac{sn^{2}}{1+n^{2}}$

library(deSolve)# 微分方程式の数値解法パッケージ

#n:個体数 k:飽和数 s:食傷捕食数 r:再生産率
parameters <- c(k = 100, s = 1, r=0.1)# パラメータのセット
initial <- c(n=5)# 初期条件
times <- seq(0, 100, 1)# 差分刻み

Ludwig <- function(t,state, parameters) {
	with(as.list(c(state, parameters)), {
		dn <- r*n*(1-n/k)-s*n^2/(1+n^2)
		return(list(c(dn)))
	})
}

# deSolveを使った数値積分を out に出力
out1 <- ode(y = initial, times = times, func = Ludwig, parms = parameters)

parameters <- c(k = 100, s = 1, r=0.2)
out2 <- ode(y = initial, times = times, func = Ludwig, parms = parameters)
parameters <- c(k = 100, s = 1, r=0.3)
out3 <- ode(y = initial, times = times, func = Ludwig, parms = parameters)
parameters <- c(k = 100, s = 1, r=0.4)
out4 <- ode(y = initial, times = times, func = Ludwig, parms = parameters)
parameters <- c(k = 100, s = 1, r=0.5)
out5 <- ode(y = initial, times = times, func = Ludwig, parms = parameters)

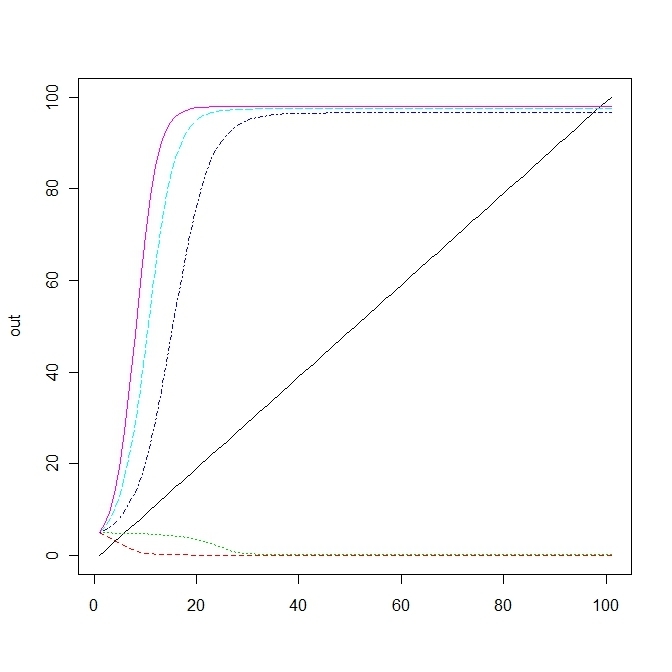
out<-cbind(out1,out2[,2],out3[,2],out4[,2],out5[,2])

matplot(out,type="l")

r=0.202前後でカタストロフィー変化が生じる
このモデルでは初期状態 $n_{0}$ と再生産率rで $\dot{n}$ の値が決まる

2016-09-01

　1.2 複雑な変化

複雑系の数理

周期関数の振幅をα倍、周期数をβ倍していき、その級数和をとると、ワイエルシュトラス関数とよばれ、
$x(t)=\sum^{N}_{j=0} \alpha^{j+1} \cos (\beta ^j t) , | \alpha | < 1$
と表せる。
ホワイトノイズはこれで表現できる。
$x( \beta t)= \alpha^{-1} x(t)- \cos(t)$
で、時間軸と関数値軸を異なるスケール変換しているので、自己アフィン相似性とよぶ。

s<-0.1
T<-1:100*s
N<-50
alpha<-2/3
beta<-2
x<-c()
ax<-c()
#x(t)の計算
for(i in 1:length(T)){f<-function(x,i){(alpha^(x+1))*cos((beta^(x))*i*s)}
                      x[i]<-sum(f(0:N,i))
                      }
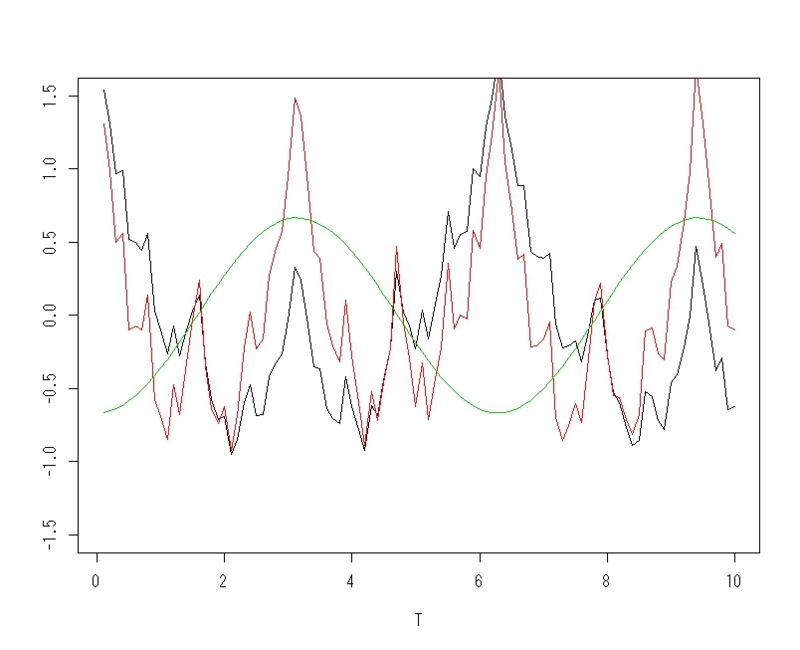
plot(T,x,type="l",ylim=c(-1.5,1.5),ylab=(""))
#αx(βt)の計算
for(i in 1:length(T)){f<-function(x,i){(alpha^(x+1))*cos((beta^(x+1))*i*s)}
                      ax[i]<-sum(f(0:N,i))
                      }
par(new=TRUE)
plot(T,ax,type="l",col=2,ylim=c(-1.5,1.5),ylab=(""))
par(new=TRUE)
#２関数の差
plot(T,(alpha*ax-x),type="l",col=3,ylim=c(-1.5,1.5),ylab=(""))

べき関数 $x(t)=A(t)t^{\gamma}$ が $\alpha x ( \beta t)=x(t)$ を満たすときの条件は
$\alpha \beta ^{\gamma}=1 , A(\beta t)=A(t)$ なので
$x(t)=t^{\frac{\log 1/\alpha }{\log \beta}} \sum^{\infty}_{j=-\infty} A_j \exp (i 2 \pi \frac{\log t}{\log \beta} j )$ と表される。
グラフとしてのフラクタル次元Dは
$D=2-\frac{\log ( 1/\alpha )}{\log \beta}$
と表される。
$H=2-D$ はハースト数とよばれる。

べき関数を $x(t)=\sum^{\infty}_{j=-\infty} A_j t^{H_j}$ と書き直すと
べき指数 $H_j=\frac{\log 1/\alpha }{\log \beta}-\frac{i2\pi j}{\log \beta}$ は複素数で、人の肺・地震・金融に応用されるらしい。

2016-09-01

　1.1 複雑な形

複雑系の数理

複雑系と呼ばれる事象は数学的にどのように認識されるのかについての本。
複雑系の数理

長さ尺度を例に。
単位尺度rを用いて、求められる長さをL(r)とする。
このとき、L(r)はrについて減少関数。
マンデルブロは海岸線について
$L(r)\approx r^{1-D}$
が成立することを発見した。
現象がべき関数であらわせるとき、べき則に従うといい、成り立つrの領域をスケーリング領域という。
上式のDをフラクタル次元という。
$L(r)=rN(r)$
とおくと、N(r)は尺度で測った回数となる。
今、rを $\frac{r}{2}$ としてみると
$L(\frac{r}{2})=cL(r)...(c \geq 1)$
となる。c=1のときは直線などの滑らかな直線のとき成り立つ。
上式は関数方程式なので、べき関数が解となる。
すると、
$D=1+\frac{\log c}{\log 2}$
と表せる。

c>1(D>1)のとき、フラクタル図形という。
1

2015-12-12

4章　Evolutionary games

Evolutionary dynamics

4.2 Nash equilibrium
２種類の生き物(もしくは戦略)A,Bがいて、AがそれぞれA,Bと出会った時の利得をa,bとし、Bの場合c,dとする。
これを↓のようなpayoff行列で表すとする。
$\matrix{ & A & B \cr A & a & b \cr B & c & d}$

このとき、
1.Aが狭義のNash均衡⇔a>c
2.AがNash均衡⇔a≧c
3.Bが狭義のNash均衡⇔d>b
4.BがNash均衡⇔d≧b

4.3 Evolutionary stable strategy(ESS)
Aが多数いる中で変異種Bがはびこらないような条件
AがESS⇔a>c or (a=c and b>d)

4.4 More than 2 strategies
strategy $S_{j}$ に対するstrategy $S_{i}$ のpayoffを $E(S_{i},S_{j})$ とする。

1.strategy $S_{k}$ が狭義のNash均衡⇔ $E(S_{k},S_{k})>E(S_{i},S_{k}), \forall i \neq k$
2.strategy $S_{k}$ がNash均衡⇔ $E(S_{k},S_{k}) \succeq E(S_{i},S_{k}), \forall i \neq k$
3.strategy $S_{k}$ がESS⇔ $E(S_{k},S_{k})>E(S_{i},S_{k}), \forall i \neq k$ もしくは $E(S_{k},S_{k})=E(S_{i},S_{k}), E(S_{k},S_{i})>E(S_{i},S_{i}), \forall i \neq k$
4.strategy $S_{k}$ が広義のESS⇔ $E(S_{k},S_{k})>E(S_{i},S_{k}), \forall i \neq k$ もしくは $E(S_{k},S_{k})=E(S_{i},S_{k}), E(S_{k},S_{i}) \succeq E(S_{i},S_{i}), \forall i \neq k$
条件の強さとして1>3>4>2

無敵なstrategyは $E(S_{k},S_{k})>E(S_{i},S_{k}),E(S_{k},S_{i})>E(S_{i},S_{i})$ で定義される

4.5 Replicator dynamics
戦略i(もしくは変異種)に対する戦略jのpayoffを $a_{ij}$ とするとn×nのpayoff行列Aができる。
また、fitnessを $f_{i}(\vec{x})=\sum^{n}_{j=1}a_{ij}x_{j}$ とすれば
再生産の方程式は $\dot{x_{i}}=x_{i}[ f_{i}-\phi]$ として表せる。

4.6 Hawk or Dove?
タカ派とハト派をモチーフにしたゲーム。
$\matrix{ & H & D \cr H & \frac{b-c}{2} & b \cr D & 0 & \frac{b}{2} }$
自分と敵のタカ派、ハト派をとる確率を $p_{1},p_{2}$ とすると
期待所得 $E(p_{1},p_{2})$ は $E(p_{1},p_{2})=\frac{b}{2}(1+p_{1}-p_{2}-\frac{c}{b}p_{1}p_{2})$ で表される。
安定点は $p^{\ast}=\frac{b}{c}$ のとき。

4.7 Thre is always a Nash equilibrium
自分も相手もn通りの戦略をとれるとし、それぞれの戦略をとる自分の分布を $\vec{p}=(p_{1},p_{2},...,p_{n})$ 、相手の分布を $\vec{q}=(q_{1},q_{2},...,q_{n})$ とする。
payoff matrixを $A={a_{ij}}$ とすれば、期待所得 $E(\vec{p},\vec{q})=\sum^{n}_{i=1}\sum^{n}_{j=1}a_{ij}p_{i}q_{j}=\vec{p}A\vec{q}$ と表せる。
このとき、 $\vec{p}A\vec{p}\geq\vec{q}A\vec{p} , \forall \vec{q}$ なる $\vec{p}$ が必ず存在する。
ペロン―フロベニウスの定理使えば証明できそう(たぶん)。

4.9 Game theory and ecology
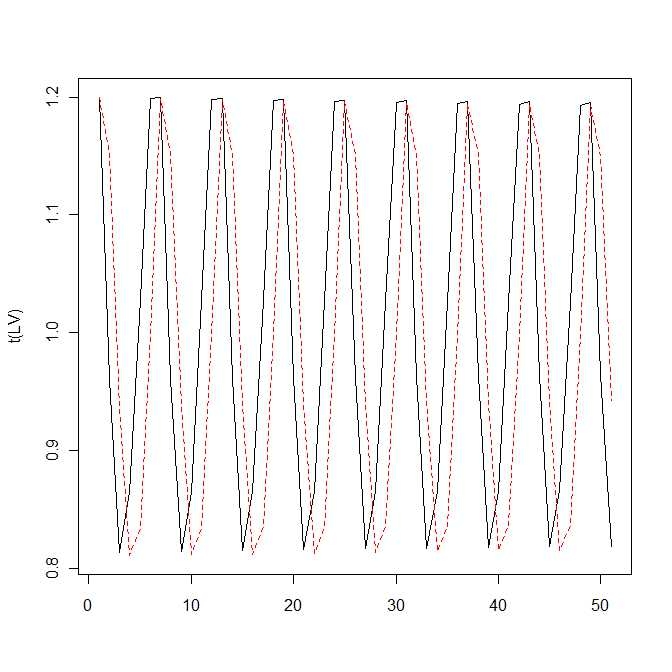
ロトカ・ヴォルテラの式について

a<-1
b<-1
c<-1
d<-1
f<-function(x,y){
x<-x+x*(a-b*y)
y<-y+y*(-c+d*x)
return(c(x,y))
}
n<-50
LV<-matrix(0,2,n+1)
LV[,1]<-c(1.2,1.2)
for(i in 1:n){
LV[,i+1]<-f(LV[1,i],LV[2,i])
}
matplot(t(LV),type="l")

2015-09-09

3章　Fitness landscape and Sequence spaces

Evolutionary dynamics

3.1 sequence space
長さLのsequenceがあったときに、有り得るsequenceは $4^{L}$ 通り。(A,T,C,G)
このL次元空間をsequence spaceとする。
これを2進数(0,1)で考えると、L次元の超立方体の格子点があり得る組み合わせとなる。
各格子点の距離はマンハッタン距離で考えられる。

3.2 Fitness landscape
Fitness landscapeはsequence space状の格子点に対し、数値(reproduction rate)を与えたもの。
各格子点の評価みたいなもの。

3.3 the equasispecies equation
2進数でのsequence spaceを考え、それぞれの格子点を10進数に変換すると0から $2^{L}-1$ まで1対1で配列番号として与える。
i番目の配列に対して、 $x_{i},f_{i},Q_{ji}$ をそれぞれiの割合、適応度、配列jからiへの変異行列とすると、
$\dot{x_{i}}=\sum^{n}_{j=1}x_{j}f_{j}Q_{ji}-\phi x_{i}$
ただし、 $\phi = \sum^{n}_{i=1} f_{i} x_{i}$
をequasispecies equationという。
Qが単位行列、つまり変異が起きないなら最も高い $f_{i}$ 　をもつ配列iが生き残る。
Qが単位行列でないなら、単体内のある点 $x^{\ast}$ 　に収束する。このときφは必ずしも最大値とはならない。
しかし、総個体数はφの指数関数で増加する。

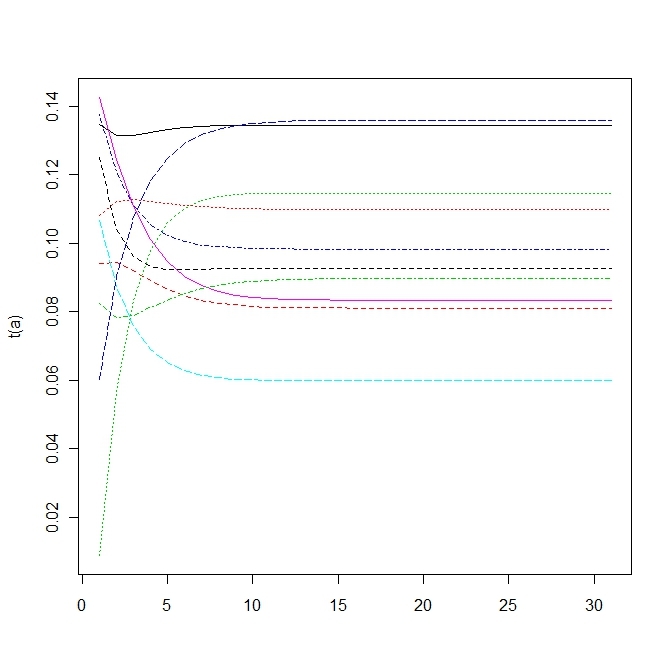
#試行回数
t<-30
#変異しうる配列数
n<-10
#遺伝子iを持つ個体の割合ベクトル
x<-runif(n)
x<-x/sum(x)
#遺伝子iを持つ個体のfittnessベクトル
f<-runif(n)
#mutation matrix
Q<-matrix(runif(n*n),n,n)
q<-apply(Q,1,sum)
Q<-Q/q
#average fittness
phi<-x%*%f

a<-matrix(0,n,t+1)
a[,1]<-x
for(i in 1:t){
dx<-(x*f)%*%Q-phi%*%x
x<-x+dx
a[,i+1]<-x
phi<-x%*%f
}
matplot(t(a),type="l")

3.4 a mutation matrix for point mutations
配列i,jのハミング距離を $h_{ij}$ として、点変異の入る確率をuとすると
変異行列Qの各成分(iからjと変異する確率)は
$q_{ij}=u^{h_{ij}}(1-u)^{L-h_{ij}}$

3.5 a adaptation is localization in sequence space
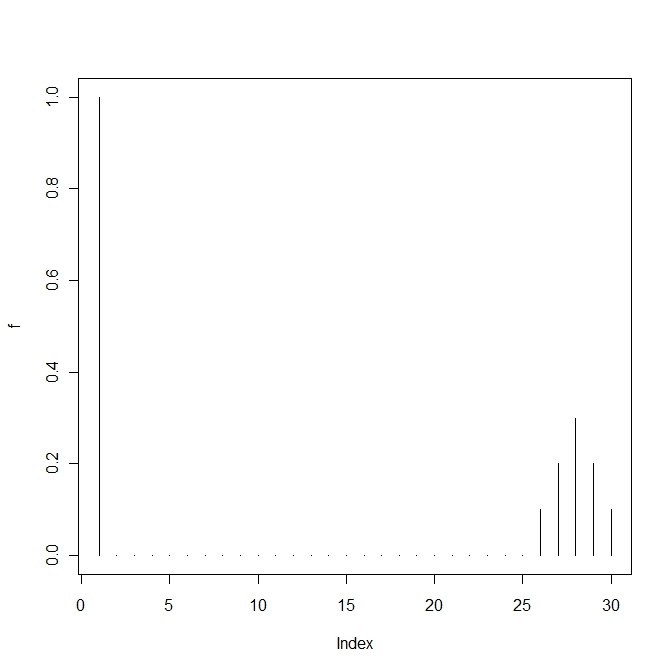
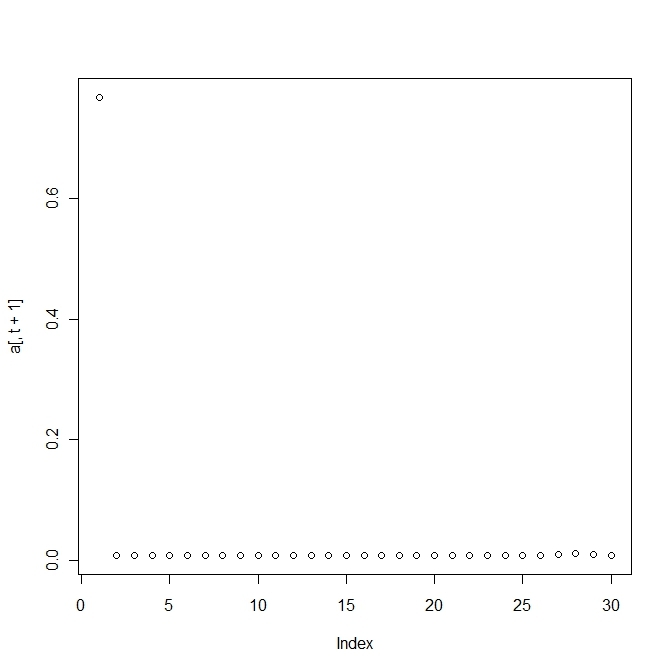
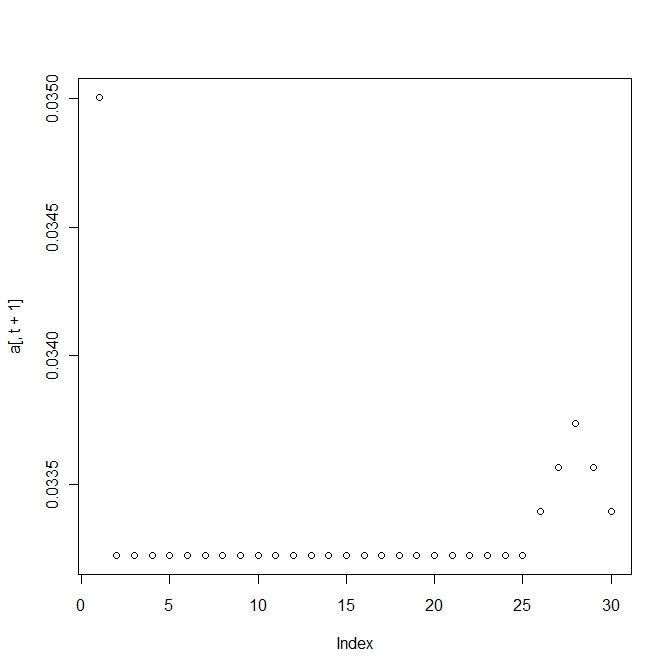
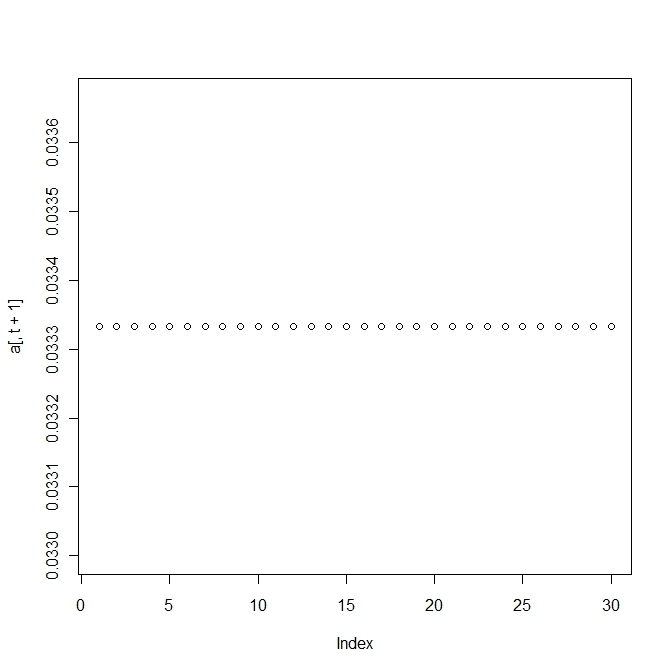
変異する確率が高すぎると適応していた個体(fittnessの値が高い)の割合がいまいち増えない。

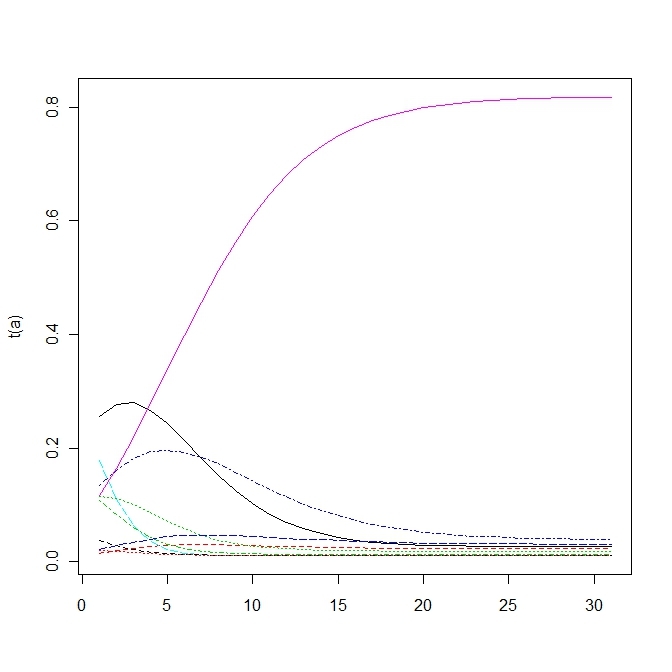
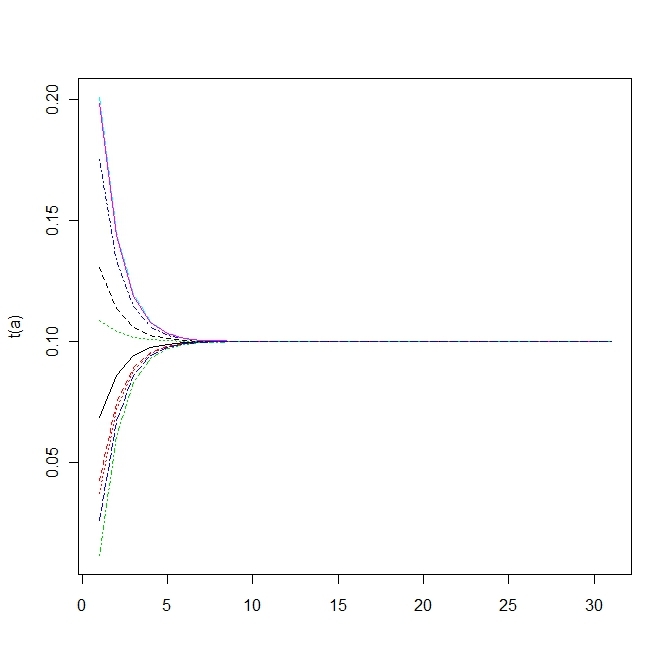
上の方は変異確率を1/100にしたもので、下の方は1/10にしたもので、上だともっとも高いfittnessをもつものに収束する。
単純なモデルでこの変異の閾値を計算すると $u<\frac{1}{L}$ 　という条件が求められる。
つまり $uL<1$ で、RNAウイルス、大腸菌、酵母菌、マウス、人などでuLの実測値が1より低いという論文が出ているらしい(Drake(1991,1998))。
一方で、QβウイルスとVZVウイルスは1よりはるかに大きく、その理由は不明。

3.6 selection of the quasispecies
2峰性のfittness landscapeをもち、1つは高いが狭く、1つは高くはないが幅広とする。
このとき、変異の割合によって生き残りが変わってくる。
変異の割合が高すぎればすべての種が生き残り、低すぎると最も高いものに収束する。
その中間であれば、2つのピークをもつ種が生き残る。

#試行回数
t<-100
#変異しうる配列数
n<-30
#遺伝子iを持つ個体の割合ベクトル
x<-runif(n)
x<-x/sum(x)
#遺伝子iを持つ個体のfittnessベクトル
f<-c(1,rep(0,n-1))+c(rep(0,n-5),0.1,0.2,0.3,0.2,0.1)
#mutationの割合を調整するパラメーター
h<-100
#mutation matrix
Q<-matrix(1,n,n)+h*diag(n)
q<-apply(Q,1,sum)
Q<-Q/q
#average fittness
phi<-x%*%f

a<-matrix(0,n,t+1)
a[,1]<-x
for(i in 1:t){
dx<-(x*f)%*%Q-phi%*%x
x<-x+dx
a[,i+1]<-x
phi<-x%*%f
}
plot(a[,t+1])

2015-08-31

2章　what evolution is

Evolutionary dynamics

evolutionary dynamicsの基本概念replication,selection,mutationについて。
replication:自己の(遺伝情報も含めて)複製。
selection:異なる個体間での淘汰。
mutation:異なる（遺伝情報をもつ）個体の生産。

1.reproduction
期間毎にそのときの個体数x(t)とある正の定数rの積で増殖するとき、
$\dot{x}=rx$
と表され、解は
$x(t)=x_{0}e^{rt}$
となる。
これと同時に、ある正の定数dで死亡するとき、
$\dot{x}=(r-d)x$
と表され、寿命の平均は $\frac{1}{d}$ となり、個体の増加率はrとなる。
$\frac{r}{d}>1$ のときに、個体数は増加していく。

最大値Kの制限付き増加モデルは、上式に制限項をかけたもので
$\dot{x}=rx(1-\frac{x}{K})$
と表され、解は
$x(t)=\frac{Kx_{0}e^{rt}}{K+x_{0}(e^{rt}-1)}$
と表される。
この解はKに収束する。

今、K=1として差分方程式を考える。
$x_{t+1}=ax_{t}(1-x_{t})$
負の値を取らない条件は $0 \leq a \leq 4$ 。
収束値 $x^{\ast}$ はaの値によって変わる。
$0 \leq a <1$ のとき、 $x^{\ast}=0$ 。
[tex:1

f<-function(a,x){y<-a*x*(1-x)
                 return(y)}
t<-50
a<-1:40*0.1
x<-0.5
X<-matrix(0,t,length(a))
X[1,]<-x
for(i in 2:t){
X[i,]<-f(a,X[i-1,])
}
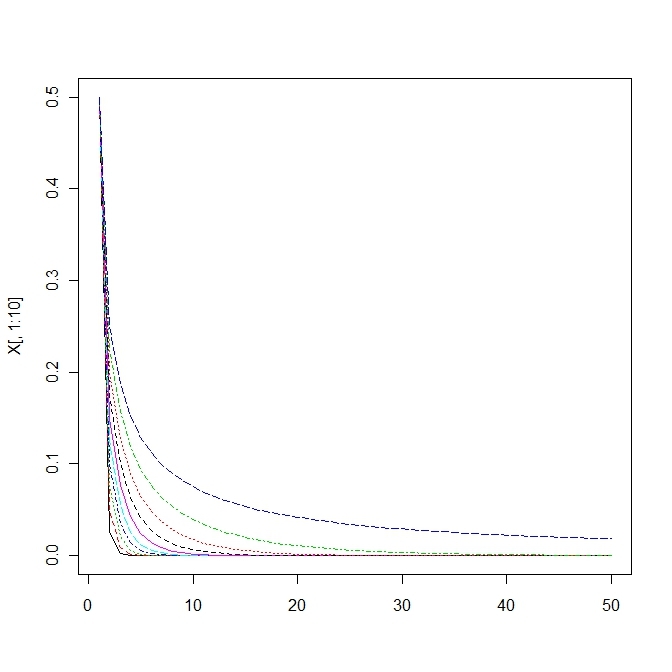
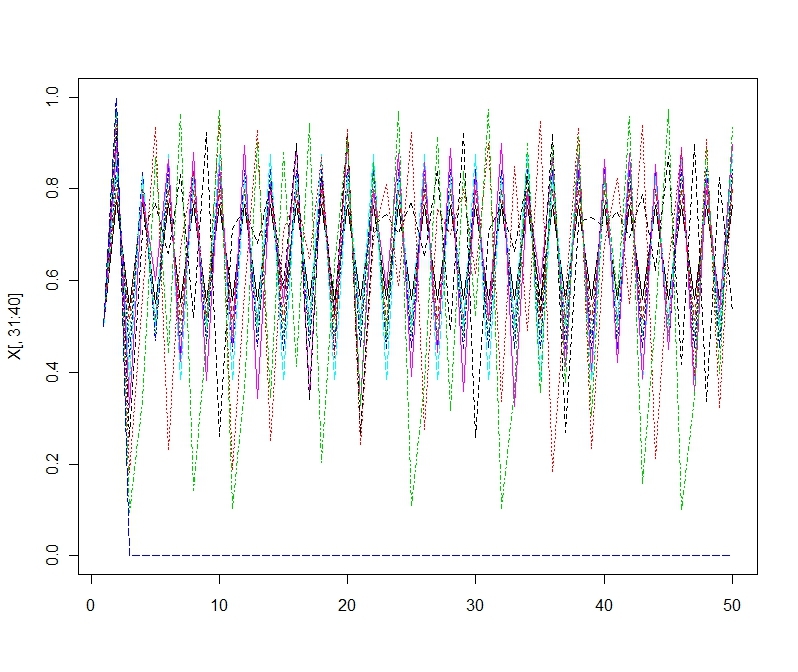
matplot(X[,1:10],type='l')
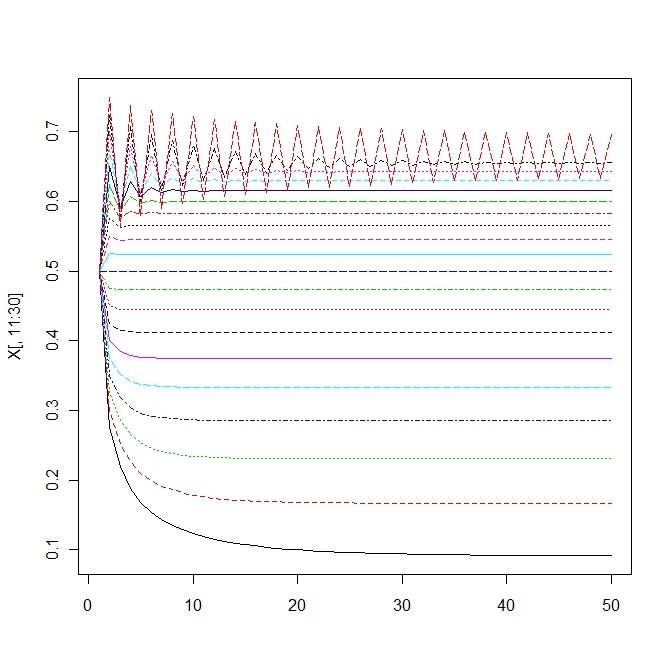
matplot(X[,11:30],type='l')
matplot(X[,31:40],type='l')

このモデルはさらに決定論的カオスで初期値鋭敏性をもつ。

f<-function(a,x){y<-a*x*(1-x)
                 return(y)}
t<-50
a<-4
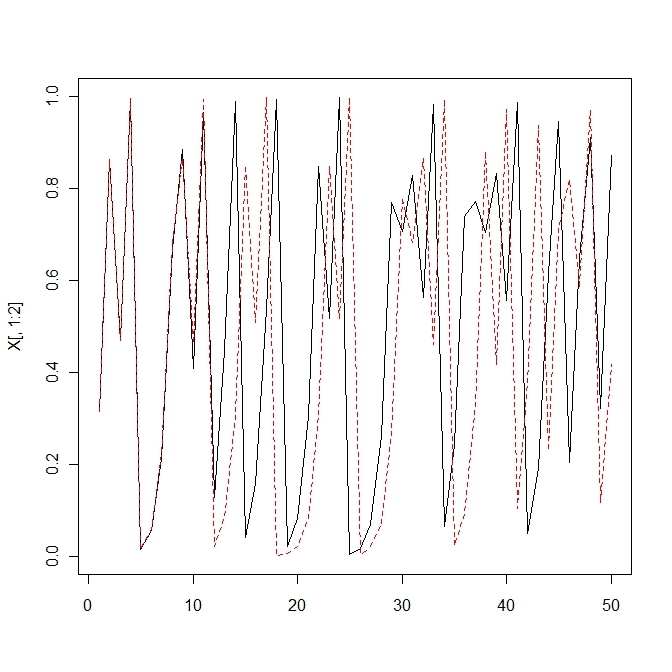
x<-c(0.3156,0.3157)
X<-matrix(0,t,length(x))
X[1,]<-x
for(i in 2:t){
X[i,]<-f(a,X[i-1,])
}
matplot(X[,1:2],type='l')

[:初期値0.3156と0.3157の挙動の違い]

2.selection
2種類の生物の個体数x(t),y(t)がそれぞれa,bの割合で初期値増殖するモデル
$\dot{x}=ax$ , $\dot{y}=by$
について
$\rho (t)=x(t)/y(t)$
とすることで、a,bの大きさで淘汰される側がわかる。

総個体数一定の条件x+y=1の下では
$\dot{x}=x(1-x)(a-b)$
が得られ、均衡は $x^{\ast}=0,1$ 。
また、a,bの大きさによって収束先が変わる。
これが適者生存の概念である。
多次元に応用すれば
$\phi = \sum{x_{i} f_{i}}$ かつ $\sum{x_{i}}=1$ として
$\dot{x_{i}}=x_{i}(f_{i}-\phi)$ とすると、
単体上で考えられる。
fが最も大きい個体に収束する。

a<-matrix(0,500,3)
a[1,1]<-runif(1)/2
a[1,2]<-runif(1)/2
a[1,3]<-1-a[1,1]-a[1,2]
f1<-1/2
f2<-1/3
f3<-1/6
S<-function(x,y,z){sigma<-sum(x*f1+y*f2+z*f3)
                    return(c(x+x*(f1-sigma),y+y*(f2-sigma),z+z*(f3-sigma)))}
for(i in 1:499){a[i+1,]<-S(a[i,1],a[i,2],a[i,3])}
library(rgl)
plot3d(a,type="l",col="2")

この３次元verでは初期状態(1/2,1/3,1/6)から(1,0,0)に収束する軌道になる。(f1が最も大きいので)

3.mutation
2タイプの個体X,Yの個体数x,yについてmutationを起こしてもう一方の個体を生む割合をそれぞれ $u_{1},u_{2}$ とすると
$\dot{x}=x(1-u_{1})+yu_{2}-\phi x$
$\dot{y}=x u_{1}+y(1-u_{2})-\phi y$
としてx,yの時間変化は表される。
$x+y=1$ とすると、 $\phi =1$ であり、
このときxの均衡値 $x^{\ast}=\frac{u_{2}}{u_{1}+u_{2}}$ となる。
3つ以上のタイプの場合、mutation matrix,Q= $[q_{ij}$ ]を用いて
$\dot{\vec{x}}=\vec{x}Q-\phi \vec{x}$ と表される。
Qはn*nの推移確率行列となる。

4.mating
閉鎖的な環境下、変異も起きない中でramdom matingが行われればallele頻度は保存される(Hardy-Weinbergの法則)