2012-12-23

関数データ解析（Machine Learning Advent Calendar 12/23）

前置き

この記事はMachine Learning Advent Calendarの12/23分の記事です。
大変申し訳ありません。時間切れでまとまっていないため、随時アップデートしていく予定です。

関数データ解析

福水先生の本をたまたま読んでいた際に出てきた「関数データ解析」という分野に少し興味を持ったので紹介させて頂きたいと思います…が、時間の都合上、詳細および「普通のデータ解析と比べてどう嬉しいのか」という話はまた次の機会とさせて頂ければ…と思います。
というかそもそも機械学習ではないのでは？という気もしますが、そこはご容赦ください。

関数データ

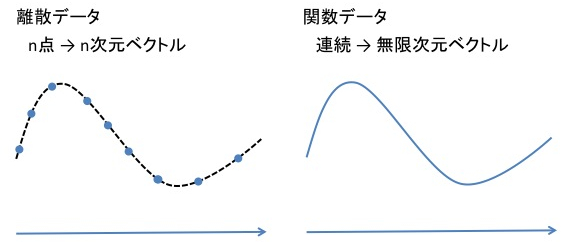
これは読んで字のごとく、関数そのものとして与えられたデータのことです。通常のデータ解析では各データはベクトル $\bf{x}$ として与えられ、データ集合 $\{\bf{x}_i\}$ に対して様々な分析を行いますが、関数データ解析では、各データは(ある区間で定義された)関数 $f_i$ として与えられ、データ集合 $\{f_i\}$ について通常のものと同じ解析を行うことを目的とします。

「関数データ」というのは、直感的には「(連続)無限次元のデータ」と思うことができます。もちろん関数が $\mathcal{R}$ 以外の値域を持つ場合などはイメージが難しくなりますが、そういう場合でも、関数たちの属する空間に一定の構造が定義されていれば分析ができる、というのが関数データ解析のいいところであり、抽象化を行う意義と言えます。

なぜ関数データか？

人間が具体的に扱える対象は高々可算個のデータであるため、関数データと言っても実際には離散的な点の集まりとしてしかデータを得ることができません。従って、関数データ解析を行うためには

離散点 $f_i^k, k=1,\cdots,K$ からなるデータの集合 $\{f_i = \{f_i^k\}\}$ を手に入れる
関数データを表現するための基底 $\{\phi_j\}$ を選ぶ
各離散データ $f_i^k, k=1,\cdots,K$ を関数データ $f(x) = \sum_j \alpha_j \phi_j(x)$ へ変換する

というような手続きが必要になり、「じゃあ結局データ点を普通にベクトルに並べてやればいいんじゃないの？」となってしまいます。それでもあえて「関数データ」として考えるのは、「モデリングが考えやすいから」というのが大きな理由ではないかと思います（論文を量産したいから、とかもあるかもしれませんが）。
例えば時系列のような、本来連続であって一連の「時間の関数」であるようなデータは、離散的な点の集まりとみなしてマルコフ的な逐次モデルでモデリングするだけでなく、時間区間全体にわたった関数であると考えてモデリングすることで、また違った解釈が可能になるかもしれないということではないかと思います。

分析を行うための「構造」

データを分析するためには、(データの属する空間に入れられた)いくつかの「構造」が必要になります。例えば、データ同士の距離とかデータベクトル同士の内積とかそういったものです。関数データ解析では、データの属する空間が関数空間(L2空間とか)なので、数ベクトルのときほど自明な構造は思いつきづらくなります。
具体的には、和と差、および内積とそれによって定まる距離が定義できれば色々な分析が可能になります（たぶん）。このような関数空間はヒルベルト空間と呼ばれるもので、関数データ解析は通常の実数空間ではなく、ヒルベルト空間の上で分析を行うものと言えます。
詳細は例によって後日とさせてください。

Functional PCA(fPCA)

関数データ解析の例として、関数データに対する主成分分析であるfPCAという方法を紹介したいと思います。
通常のPCAでは標本相関行列
$\rho_{ij} = \frac{1}{N}\sum_k (x_k^i - \bar{x}^i) (x_k^j - \bar{x}^j)$
( $x^i$ は $x$ の $i$ 成分を表す)の対角化を行い、固有値・固有ベクトルを求めます。同じ考え方を関数データに適用すると、相関行列は相関関数となり
$\rho(s,t) = \frac{1}{N}\sum_k (f_k(s) - \bar{f}(s)) (f_s(t) - \bar{f}(t))$
となります。これは[-1,1]の値をとるs,tの関数となり、これを対角化する関数 $\phi$
$\int dt \rho(s,t) \phi(s) = \lambda \phi(t)$
を求めることでfPCAの固有関数を求めることができます。
ただし、多くの場合は関数データを表現する際に使った（有限個の）基底を用いて固有関数自体も展開してやることで、通常のPCAのように行列演算で解くこともできます（参考文献3-1）。

申し訳ありませんが、ここで一旦公開とさせて頂ければと思います。具体例については、後日補足したいと思います。

参考文献

入門的資料
1. Functional Data Analysis: A Short Course
再生核ヒルベルト空間(RKHS)の枠組みできちんと議論しているもの
1. Nonlinear Functional Regression: a Functional RKHS Approach
2. An RKHS Framework for Functional Data Analysis
fMRIの画像データに対して関数データ解析を行っているもの
1. Functional Principal Component Analysis of fMRI Data
日本語の文献（後ろの章に少し取り上げられています）

カーネル法入門―正定値カーネルによるデータ解析 (シリーズ多変量データの統計科学)

作者: 福水健次
出版社/メーカー: 朝倉書店
発売日: 2010/11/01
メディア: 単行本
クリック: 19回
この商品を含むブログ (11件) を見る

2012-11-16

ハイブリッドモンテカルロを実装してみた

R データ解析機械学習・統計

恐ろしく久しぶりですが…。
PRMLの後ろの方にあるハイブリッドモンテカルロのところを読んでいて、実際どんな動きをするのかと思い実装してみました。
以下コードと結果。

# set any function (exp(-energy) should be relevant distribution)
energy <- function(z){
  z*(z-1)*(z-4)*(z-6)/12
}

# set derivative of function "energy" (make sure the function is vectorized)
dzenergy <- function(z){
  ((z-1)*(z-4)*(z-6) + z*(z-4)*(z-6) + z*(z-1)*(z-6) + z*(z-1)*(z-4))/12
}

#leapfrog integral
leapfrog <- function(z0, r0, dzenergy, epsilon, nstep){
  z <- z0
  r <- r0
  log <- c(z0,r0,0.5*(r%*%r)+energy(z))
  for(i in 1:nstep){
    r <- r - 0.5*epsilon*dzenergy(z)
    z <- z + epsilon*r
    r <- r - 0.5*epsilon*dzenergy(z)
    log <- rbind(log, c(z,r,0.5*(r%*%r)+energy(z)))
  }
  return(list(z,r,log))
}

#hybrid montecarlo sampling
hybridMontecarlo <- function(z0, energy, dzenergy, nloop, epsilon, nLFstep){
  z <- z0
  sample <- z
  log <- as.list(NULL)
  for(i in 1:nloop){
    # initialize
    r <- rnorm(length(z))
    H <- 0.5*(r%*%r) + energy(z)

    # leapfrog
    new <- leapfrog(z, r, dzenergy, epsilon, nLFstep)
    znew <- new[[1]]
    rnew <- new[[2]]
    log[[length(log) + 1]] <- new[[3]]

    # metropolis
    Hnew <- 0.5*(rnew%*%rnew) + energy(znew)
    dH <- Hnew - H
    if(dH < 0 || runif(1) < exp(-dH)){
      z <- znew
      sample <- rbind(sample, z)
    }
  }
  return(list(sample, log))
}

# only for 1 dimensional sampling
test <- function(z0, nloop, eps, nLFstep){
  s <- hybridMontecarlo(z0, energy, dzenergy, nloop, eps, nLFstep)

  X11()
  smin <- min(s[[1]])
  smax <- max(s[[1]])
  hist(s[[1]], xlim=c(smin,smax))
  par(new=T)
  plot(function(z)(exp(-energy(z))), xlim=c(smin, smax), col="red", ann=F, yaxt="n")
  
  X11()
  rmin <- min(s[[2]][[1]][,2])
  rmax <- max(s[[2]][[1]][,2])
  ptim <- seq(1,nloop,20)
  for(i in 1:length(ptim)){
    plot(s[[2]][[ptim[i]]][,1], s[[2]][[ptim[i]]][,2], xlim=c(-1,7), ylim=c(rmin,rmax), col=i, xlab="position", ylab="momentum")
    par(new=T)
  }

  return(s)
}

上の図はサンプル結果と真の分布、下の図はサンプル過程（リープフロッグ積分）での各粒子（サンプル点）の相空間中の動きです（ただし20回に1回だけ描画）。
ハイブリッドモンテカルロは、要するに

ギブス分布の空間座標についての周辺分布が欲しい分布となるようなポテンシャル関数を設計する。
- $V(x)=-\log p(x)$ となるポテンシャルを用意する（分配関数は定数なので無視できる（エネルギーの原点はどうでもいい））。
適当な運動量(普通はN(0,1)に従う)を持つ粒子群を生成し、上記のポテンシャルの下で物理系をシミュレートする（微分方程式を解く。普通は正準方程式をリープフロッグ積分で解く）。
適当なタイミングで系のスナップショット（アンサンブル）をとって、運動量について周辺化する（ヒストグラムをとる）と欲しい分布が得られる。

という考え方で（実際は積分誤差を補正するためのメトロポリス棄却なんかが入っています。コード参照。）、エルゴード性そのもの！という感じでハァハァしますね。
普通のMCMCでは提案分布からの乱数でステップを更新するのに対して、ハイブリッドモンテカルロではステップを求めるために微分方程式を解いて力学系をシミュレートする必要があるので（その分自己相関の低いステップが早く得られるのですが）、高次元ではなかなか厳しそうです。

メトロポリス棄却のところは、物理系のシミュレートは当然ながらエネルギーが保存するように行わなければならない（物理法則を破ってしまう）のに対し、リープフロッグ積分の数値誤差でどうしても保存しなくなってしまうため、そのような場合を棄却する効果を果たします。と言いつつ、エネルギーが減ったプロセスについてはアクセプトするようで、いまいちどういうものなのかよくわかっていません…。

テストコードのエネルギー関数はhttp://d.hatena.ne.jp/n_shuyo/20100609/hybrid_mcから引用させて頂きました。ありがとうございます。

2012-07-01

windows7 64bit環境でのpython, opencvセットアップ等

python cv win

かなり久しぶりの記事になってしまいました。

windows7 64bitで環境構築にずいぶん手間取ったのでいくつかのポイントをメモしておきます。
目標は、64bit版のpythonやopencv(含むpython バインディング)あたりが普通に使えるようになることです。

pythonのインストール

python自体のインストールは公式サイトから配布されているインストーラを使えばできるはずです。
インストールしたらPYTHON_HOME環境変数にpython.exeがあるディレクトリを設定し、PATHに%PYTHON_HOME%を追加しておきます。

easy_install(setuptools)のインストール

pyhonのパッケージ管理システムにはeasy_installとpipがありますが、pipを入れるのにeasy_installがあった方がよいのでまずインストールします。これも公式の指示に従えばOKですが、サイトに書いてある通り、64bitの場合はインストーラがないのでez_setup.pyをダウンロードして実行することでインストールします。
easy_installは%PYTHON_HOME%/Scripts以下にインストールされるはずなので、ここにもPATHを通しておきます。

pipのインストール

easy_install pip

でOK

numpy, scipyのインストール

これらが少々面倒です。計算をするならnumpy, scipyは入れておきたいですが、一筋縄ではいかなくなります。
まず、

pip install numpy

とすると、いくつかエラーが出るはずで、その内容は

BLAS/ATLASがない
Lapackがない
vcvarsall.batがない

というものになるはずです。BLAS/ATLAS, Lapackを64bit環境でビルドする必要がありますが、そのためにはfortran コンパイラが必要で、ではMSYSやCygwinで64bitに対応してビルドするにはどうするか…という面倒な問題になります。また、vcvarsall.batはVisualStudio2008(EEでよい)が必要で、2010だけではビルドできません。(参考)
こういった面倒な状況に対応してくれている素晴らしいサイト(gohlke)があります。ここではpython関連の各種パッケージを32bit,64bitそれぞれのwindows向けにビルドしたインストーラを配布してくれています。numpyやscipyもあるので、これを利用するのがおそらく最も確実です。
さらに、ここで配布されているnumpyはIntel MKLでビルドしたもの(そうでないものもありますが、ここのscipyバイナリのインストールにはMKL版numpyが必要)なので、計算速度の観点からも是非これを使うべきと言えます。

matplotlibのインストール

綺麗なグラフを書きたいとなると必要なんですが、これがまた超頻出のハマリパターンがあるようで、しっかりハマると思われます。

pip install matplotlib

とすると、(VS2008がなければ)先ほどと同じ「vcvarsall.batがない」というエラーが起こり、あったとしてもmatplotlib.ft2font関連でエラーが起こると思われます。これについては"matplotlib ft2font"などでググると大量の事例が見つかり、freetype2フォントを別にインストールすることで何とかなったりもするようですが、freetype2フォント自体はwindows向けのバイナリが公開されておらず、自前の64bit環境でビルドする必要があります。
これについても、パッケージ管理システムを使うのはさっさと諦めて(ただしeasy_installを使うとうまくいくかもしれません。その場合もvcvarsall.batは必要)、公式のインストーラを使うのが早いと思います。

OpenCVのインストール

ここでpythonから一旦離れて、OpenCVを64bit環境にインストールします。以下の説明は基本的に公式のインストールガイドの通りです。

cmakeのインストール

64bit版のOpenCVは自前でビルドする必要があり、環境に合わせてVisualStudioのプロジェクトファイル(またはMakefile)を生成するためにcmakeを用いる必要があります。というわけで、まずは公式からcmakeのインストーラを落としてきてインストールします(cmake自体は32bit版しかない)。インストーラにcmake.exeの場所へPATHを通すか聞かれるので、通しておくと良いです。

OpenCVのインストール

cmakeをインストールしたら、ビルドするOpenCVのソースをこの辺りから落としてきます。通常は最新版を落とします。OpenCV-2.4.1.exeなどのファイルがそれで、自己解凍形式になっているので適当な場所へ解凍します。
解凍したらcmake guiを起動し、Where is the source code:に解凍してできたディレクトリ(CMakeLists.txtがあるディレクトリ)、Where to build the binaries:にその直下のbuildディレクトリを指定してConfigureを押します。するとgenerator(コンパイル環境)を聞かれるので、VisualStudio10 Win64(VisualStudio2010を使っているなら)を指定します。

VisualStudioがExpress Editionの場合、64bitプロジェクトをビルドするのに若干の設定がいる場合があります。基本的にはVisualStudioとは別にWindows SDK 7.1をインストールすればOKですが、VisualC++の修正とWindows SDKの相性が悪くインストールできない場合があり、その場合はこの記事の内容に従う必要があります。

無事configureが終わるとビルド設定の画面が出てきますが、opencv.jpあたりの記事を参考に、自分の環境に合わせてせっていします。ここで、tbb、Eigenあたりをインストールしておくとよいと思います。特にtbbは簡単な(C++)テストプログラムを試す際にも要求されることがあるようです。tbbは適当な場所に解凍し、tbb40\bin\intel64\vc10あたり(dllファイルのある場所)、tbb40\include\tbbあたり(ヘッダファイルのある場所)にPATHを通します。また、Eigenはテンプレートライブラリなので、(C++であれば)必要なときにヘッダファイルを読み込むだけで利用できます。解凍したディレクトリにPATHを通します(PATHを通したディレクトリ\Eigen以下に.hなしのヘッダファイルがあります)。
また、cuda込みのビルドは手元ではどうにもうまく行っていません…(こういう感じの問題が起こる)。

ビルドされたライブラリとヘッダファイルのディレクトリにパスを通し、VisualStudioで(例によって)追加ライブラリにopencv_core241.lib, opencv_highgui241.lib, opencv_imgproc21.libあたりを追加して適当なテストプログラムがビルドできればとりあえず完了です。

Python バインディングのインストール

cmakeの設定でPython用のビルドを含める設定をしていれば自動的にcv2.pydがビルドされているはずなので、これをpythonから見える場所にコピーすればOK…のはずですが、うまく行かない場合があるようです。その場合は例によってgohlkeからバイナリをダウンロードしてきてインストールするとうまく行くと思います…。

VisualStudioの有償版があれば64bit環境に関する色々なところがだいぶ楽になりますが(それでもハマる)、EEでは色々と罠が多かったです。基本的に、ビルドを伴うパッケージの場合はpipだとハマる可能性が高そうです。

2012-04-15

opencvのpythonバインディングメモ

python cv

すぐ忘れるのでメモ。

画素値(x,y)を取得する

cv.Get2D(img,y,x)

画像サイズ(Lx,Ly)を取得する

cv.GetSize(img)

画像を作成する

cv.CreateImage((Lx,Ly), nbit, nch)

x,yがどっちがどっちかすぐ忘れる。
以下追記。

2012-01-04

前に作ったRでisomapのコード

R 機械学習・統計 C++

前にTokyo.Rで発表したisomapのコード、どこにも公開していなかったので、githubに上げてみました。
https://github.com/kohta/Risomap
微妙に計算を工夫しているので、veganパッケージに入っているisomapより2倍くらいは速いはず…。
発表資料等については下記のエントリを参照ください。
http://d.hatena.ne.jp/koh_ta/20110528/1306595492

2011-12-22

Rでfor文は使うべきでないか？ (R Advent Calendar 2011)

この記事はR Advent Calendar 2011 (http://atnd.org/events/22039)への参加記事です。

Rではよく「for文は使うべきでない」と言われます。forではなく、ベクトル単位での処理として記述したり、lapplyやapplyなどのベクトル・行列に対するmap系関数を使うべきとされています。しかし実際には、必ずしもいつもfor文を避ければ良いというものでも無いようです。今回はそのあたり、for文がどのくらい遅いのか(または遅くないのか)を調べてみたいと思います。

lapply関数

通常、for文と対応関係にあるのはlapply関数です。lapplyは

lapply(v,func)

という形で用いられ、その機能は

第一引数のベクトルvの各要素にfuncを適用する
各要素への適用結果をリストにまとめて返す

というものです。
for文で書ける処理はlapplyでも書くことができ、以下のようになります。

for(i in 1:n){
  func(i) #なんらかの処理
}

lapply(1:n,func)

以下ではforとlapplyの速度が、使用ケースによってどのように異なるかを見ていきます。

もったいぶってもあれですので、ネタバレすると次のような構成で話をします。

何もしないforループとlapplyの関係

forループとは異なり、lapplyは「何もしない」場合でも関数呼び出しが必要であり、その分forよりも大分遅くなります。

forにも同等の関数呼び出しが含まれる場合は、lapplyの方がわずかに速くなります。

リストを返すループ

lapplyではループ処理を行った結果をリストに格納して返します。結果を捨てるようなforループと比較するとlapplyは遅くなります。

一方、for文で同様のリスト生成を行おうとするとlapplyに比べ圧倒的に低速となります。

ベクトル演算とforループ

R組み込みのベクトル関数の処理をforループで実現しようとすると圧倒的に低速となります。これは、lapplyの場合と同じく、処理がどこまでC言語実装に含まれているかの問題です。

結論として、「可能な限りC言語実装の関数を使うべき」であり、「無駄な処理の含まれるC言語実装関数は無理に使うべきでない」となります。

テスト関数

テストのため以下のような関数を用意しています。テスト対象の関数funcとテストケースcasesを渡すことで処理時間を測定します。

tester <- function(func,cases){
  results <- c()
  results.names <- c("user","system","elapsed")
  for(case in cases){
    result <- system.time(func(case))
    results <- c(results,result[1:3])
  }
  results <- matrix(results,ncol=3,byrow=T)
  colnames(results) <- results.names
  return(results)
}

何もしないforループとlapply

まずは何もしないforとlapplyについて比較してみます。

cases <- list(1:10^7,1:(2*10^7),1:(3*10^7))

test.lfor.null <- function(v){
  for(i in v){}
}

empty.func <- function(x){}
test.lapply.empty <- function(v){
  lapply(v,empty.func)
}

テスト結果は次のようになります。

> test.lfor.null.result
      user system elapsed
[1,] 0.095      0   0.095
[2,] 0.188      0   0.189
[3,] 0.284      0   0.284

> test.lapply.empty.result
      user system elapsed
[1,] 0.371  0.004   0.375
[2,] 0.740  0.006   0.746
[3,] 1.118  0.003   1.121

for文の方が４倍程度速いという結果になりました。これはlapplyでは処理を関数に包む必要があり、必ず関数呼び出しのコストがかかるためです。実際、for文の方にも関数呼び出しのコストを乗せると

test.lfor.empty <- function(v){
  for(i in v){
    empty.func(i)
  }
}

> test.lfor.empty.result
      user system elapsed
[1,] 0.500  0.002   0.502
[2,] 0.984  0.007   0.992
[3,] 1.470  0.007   1.478

となり、lapplyの方が1.3倍程度速くなります。
従って

関数に包む必要のない処理についてのループでは、for文を使う方が良い

と言えそうです。

何かするforループとlapply

次に、ループ内で何らかの処理をする場合の速度を比較してみます。
ここでは、単純に足し算を行うだけの処理とします。

cases <- list(1:10^7,1:(2*10^7),1:(3*10^7))
plus1.func <- function(x){1+1}

test.lfor.plus1 <- function(v){
  for(i in v){
    plus1.func(i)
  }
}

test.lapply.plus1 <- function(v){
  lapply(v,plus1.func)
}

> test.lfor.plus1.result
       user system elapsed
[1,]  8.806  0.416   9.224
[2,] 15.874  0.017  15.898
[3,] 24.569  0.251  24.829

> test.lapply.plus1.result
       user system elapsed
[1,] 13.626  0.204  13.835
[2,] 30.235  0.519  30.765
[3,] 40.767  3.523  55.877

今度はlapplyの方がかなり遅くなりました。これはlapplyの「結果をリストとして返す」機能のせいだと考えられます。forでは足し算の結果をその都度捨てていますが、lapplyでは逐一リストに追加し、結果として返す操作が加わっています。
for文を使って明示的にリストを生成してみるとどうなるかというと

cases.small <- list(1:10^4,1:(2*10^4),1:(3*10^4))

test.lfor.plus1.list <- function(v){
  result <- list()
  for(i in v){
    result <- c(result,1+1)
  }
  return(result)
}

> test.lfor.plus1.list.result
       user system elapsed
[1,]  2.678  0.090   2.774
[2,] 11.673  0.837  12.558
[3,] 25.148  1.882  27.042

これまで使っていたcasesでは時間がかかりすぎるため、小さいケースで実行しました。ループ数が3桁小さいにも関わらず、lapplyの場合の半分程度の時間がかかっています。すなわち、lapplyで行ったリスト生成と、Rで明示的に記述したリスト生成とでは数百倍程度の速度差があるということが分かりました。
lapplyはRの組み込み関数でありその実装はC言語です。リストの生成操作もC内部で行われており、この部分がpure Rでのリストを返す関数との決定的な速度差を生んでいると考えられます。

リストを生成するような処理は可能な限りlapplyで行うべき

と言えます。

ベクトル演算とforループ

最後に、より基本的なテクニックとしてベクトル演算とforループの比較をしてみます。

vs <- list(1:10^7,1:(2*10^7),1:(3*10^7))

test.vfor <- function(v){
  for(i in v){
    i + 1
  }
}

test.vector <- function(v){
  v + 1
}

> test.vfor.result
       user system elapsed
[1,]  4.391  0.050   4.441
[2,]  8.698  0.030   8.727
[3,] 12.863  0.015  12.879

> test.vector.result
      user system elapsed
[1,] 0.032  0.000   0.032
[2,] 0.079  0.043   0.122
[3,] 0.117  0.065   0.182

これは(当然ながら)組み込みのベクトル演算を利用した方が圧倒的に高速です。lapplyの場合と同じように、ループ処理がC言語実装の内部に含まれているためです。

結論

以上の比較から、「Rではfor文を使うべきではない」という説については

ループ内の処理を関数に包む必要がない場合はfor文の方が良い
リスト生成の必要がないループについてはfor文の方が良い
リスト生成、ベクトル演算など、組み込みのループ処理を利用できる場合はそれを用いた方が良い

と言えるだろうと考えられます。結局いかにCで実装された関数を利用できるかという問題ですが、C実装の関数も完璧ではなく、場合によっては不要な処理が含まれていたり、データ構造を上手く処理できない場合などもあります。基本的な特性を押さえつつ、ケースバイケースで使い分ける必要があると言えそうです。

多次元の場合

（Rで多次元ループを書く機会はそれほど多くない気もしますが）多次元の場合も基本的には同じで、いかに組み込みのC実装関数を使うかがポイントとなります。詳しくは下記の参考文献(Chapter 14)を参照して頂きたいのですが、特に注意すべき点として

applyはC実装ではなくR上での実装である

という点があります。行列型に整形したデータについてapplyを使えば自動的に速くなるというわけではなく、いかにベクトル演算を使うかという点に注意してコーディングする必要があります。

追記

for文でlistを生成するところについて、yatsutaさんからコメントを頂きました。forの方ではループコストの差異に加えlistの領域を確保するコストが上乗せされている、というものです。これを考慮するには、forで逐次的にリストを大きくしていくのではなく、予め必要なサイズを確保しておいた上で要素のセットにforループを使う必要があります。
実行してみると下記のようになります。

vs <- list(1:10^7,1:(2*10^7),1:(3*10^7))

test.lfor.plus1.list2 <- function(v){
  result <- vector("list",length(v))
  for(i in v){
    result[[i]] <- 1+1
  }
}

> test.lfor.plus1.list2.result
       user system elapsed
[1,] 37.215  0.287  37.503
[2,] 61.647  1.017  63.459
[3,] 90.967  3.785 102.298

元のサイズのテストケースで実行することができ、速度はlapplyの場合の1/2程度となりました。逐次的にlistを拡大していったケースのコストは、ほぼ全てがlistのための領域確保コストであったことになります。
領域確保コストを除いてもforの方が2倍程度遅いということになりましたが、この原因は「ループそのもの」と「代入」による速度差を合わせたものとなります。これらを個別に見るのは、ループまたは代入のみをC実装で行うような関数が(おそらく)Rには無いため、中々難しいかと思います。とはいえ、両方合わせてこのくらいの差があると把握しておけば実用上は十分そうです。

参考文献

プログラミング的な側面からRを解説した資料はあまり多くありませんが、最近出た以下の本は、おそらく本としては最もこの手の話題について詳しいのではないかと思います。Rコードの書き方と速度の関係についても1章割かれています。

The Art of R Programming: A Tour of Statistical Software Design

作者: Norman Matloff
出版社/メーカー: No Starch Press
発売日: 2011/10/11
メディア: ペーパーバック
購入: 2人クリック: 62回
この商品を含むブログを見る

2011-11-05

非線形連続フィルタリング問題と経路積分

物理情報

クローズドでやっているアカデミック寄りの勉強会で発表しました。
マニアックな内容なので自分用の記録ということで…。

個人的に興味があって少し調べたりしていた経路積分を応用した各種手法に関するものです。
昔からある非線形連続フィルタの問題（線形の場合はKalman-Bucyフィルタといいます）についてで、割と最近の成果として唯一実用的に非線形連続問題に対応できる（と主張されている）Yau equationの解を形式的に経路積分表示で書くことができるというものです。
実用例については調べきれていませんが、経路積分表示を用いて物理系（ラグランジアン）との対応関係を考えることで近似や摂動が考えやすくなるという利点があると思われる一方、パスサンプリングなどが現実的に計算できるのかといった問題が出てくると思います。
また、似た問題として確率的最適制御問題の解を経路積分で書くという話も少し話しました。こちらは実際に物理系のコンテキストでの近似の適用例などが原論文に出ています。資料では書ききれていませんが…。

専門分野というわけでは無いので穴もあり色々突っ込みをもらいました…。こちらからも疑問点として挙げていた、あらゆる確率過程（ウィーナー過程）でモデル化される問題の解を経路積分で書くことはできず何らかの条件が必要になる、という点についてはもう少し考えてみたいと思っています。

が、当面はもう少し実際的な分野に力を入れる方向で…。

Nonlinear Filtering and Path Integral Method (Paper Review)

View more presentations from Kohta Ishikawa

前置き

関数データ解析

関数データ

なぜ関数データか？

分析を行うための「構造」

Functional PCA(fPCA)

参考文献

pythonのインストール

easy_install(setuptools)のインストール

pipのインストール

numpy, scipyのインストール

matplotlibのインストール

OpenCVのインストール

cmakeのインストール

OpenCVのインストール

Pythonバインディングのインストール

lapply関数

テスト関数

何もしないforループとlapply

何かするforループとlapply

ベクトル演算とforループ

結論

多次元の場合

追記

参考文献

Python バインディングのインストール