インポート状況→インポート完了
記事とコメントのインポート完了。
- インポートページ ログイン - はてな
メイヤー系とコ/モナド
記法:
ベックの分配系は4種類あって、
3,4番の分配系を混合分配系と呼ぶ。1,2番は非混合分配系〈unmixed distributive system〉。
分配系の一番目の構成素(コ/モナド)に対して、そのアイレンベルク/ムーア圏を作る。二番目の構成素(コ/モナド)は、そのアイレンベルク/ムーア圏上のコ/モナドに持ち上がる。Yを二番目のコ/モナドとして、持ち上げをY↑δと書く。Y↑δに対して再びアイレンベルク/ムーア圏を作る。
以上の手順で出来た圏を分配系のアイレンベルク/ムーア圏とする。
非混合分配系の場合は複合コ/モナドが作れて、それのアイレンベルク/ムーア圏を作ればいいが、混合分配系の場合は複合系が作れない! 上記の持ち上げ方式だと、混合系を経由しないでアイレンベルク/ムーア構成ができる。
複合系が要らないので、自由にアイレンベルク/ムーア構成ができて、第一コ/モナドと第二コ/モナドの区別もシッカリできる。複合系を一般化してもアイレンベルク/ムーア構成は出来るかも知れない。
コマンド・クエリー分離されたメイヤー系は、コマンド・モナドのスタンピングによるモナドと、値の余代数スタンピングによるコマンドが作る、モナド・コモナド分配系になる。よって、そのアイレンベルク/ムーア圏が作れる。アイレンベルク/ムーア圏の対象は、モノイドが作用する状態空間(ラベル付き遷移系)に、クエリー構造を付けたもの。クエリー構造がコモナドの余代数であることから、副作用なし(余単位律)と内部生(余結合律)が出てくる。
メイヤー分配系の単一複合系は作れないので、持ち上げによって階層的に(繰り返しにより)定義するしかない。
シーケントの役割、使い所
形式/非形式とレイヤー構成 - 檜山正幸のキマイラ飼育記 メモ編にシーケントが出てこないが、シーケントは構文形式なので、幾つかの使い途がある。
- 基本推論図は、ひとつのシーケントで表現可能で、基本推論図とそのシーケントは同一視してもよい。
- 一般の推論図のプロファイルはシーケントで表現できる。
- 省略したリーズニング図は、シーケントと基本リーズニング図で出来ている。
形式/非形式とレイヤー構成
| 大分類 | 非形式 | 形式化データ | 備考 |
|---|---|---|---|
| 計算 | 対象式 | 対象式(項) | もともと形式化されている |
| 論理 | 命題 | 論理式 | 文字列または構文解析木 |
| 論理 | 推論 | 推論図 | 仮定と結論がある |
| 論理 | リーズニング | リーズニング図 | ツリー状ノード・ワイヤー図 |
すべての形式化データは、ノード・ワイヤー図で表現される。推論図は2次元的な構造を持ち、その構文解析木がリーズニング図(の木)で与えられる。レイヤーは多いが、やってることは同じことの繰り返し。
すべてのデータはグラフ/ツリーなので、グラフ/ツリー処理言語があれば操作可能。実質的にツリーだと思ってよいので、ツリー処理言語。ツリー処理言語を使った計算をツリー算術と呼ぶ。
ツリー算術は計算レイヤーに落ちるので、レイフィケーション構造を作れる。レイフィケーション構造=ゲーデル構造。プログラミング的に言うと、レイフィケーション構造はリフレクションライブラリ/メタプログラミングライブラリ/メタオブジェクト・プロトコール。
律子と制約と一貫性
「一貫性」という言葉が曖昧だから整理する。
まず、律子〈rator〉は法則を与える2-射(あるいはもっと高次の射)のこと。律子が満たす等式を制約等式〈constraint equation〉または等式的制約〈equational constraint〉または単に制約〈constraint〉と呼ぶ。ここまでは特に「一貫性」という言葉は出てこない。
が、制約を一貫性制約と呼ぶことがある。ちょっと違うような気がする。一貫性は、「律子+制約」がある状況で、律子達で作った自由圏がやせていることだろう。つまり、一貫性、あるいは「一貫性がある/を持つ」のような言い方は、「律子+制約」が作る構造に対する形容詞なのだと思う。
よって、一貫性制約の意味は、「一貫性を持つ『律子+制約』の制約」だろう。一貫性を持つようにうまく定義されている制約、という感じか。
一貫性定理は、特定の「律子+制約」構造が実際に一貫性を持つことを主張する定理。
一貫性法則〈coherence law〉が一番意味不明で、制約等式のことか、一貫性定理のことか不明。
随伴の方向の事例
随伴に関する注意事項 - 檜山正幸のキマイラ飼育記に関連して:
次の例は、http://www.math.uchicago.edu/~may/VIGRE/VIGRE2011/REUPapers/Berger.pdf から。ここ(以下のコピーのところ)で初めて記号'-|'が出てきている。
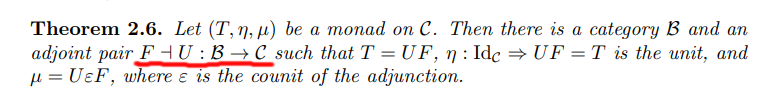
随伴系の方向はペアの右の関手に合わせている(しばらく考えると分かる)。
問題集11「小学生でも…」の解答と補足説明 (A23R11)
※この記事は「記事23 問題集11の解答」
問題集11とは、次の記事(の問題部分)のことです:
上記記事への追記で次の文言を入れました。
「全部乗せで、完全にグラフィカルなリーズニング図」を描くのはムチャクチャ大変だわー。ゴメン、そこまでやんなくていいわ。真面目にやると、どの程度の労力と面積が必要かの見当がついたら、あとはテキトーに手を抜いていいです。
やっぱり、ガッツリ完全に描画はシンドすぎる。このシンドさを実感すれば、どうして省略記法しか使われないか、の理由も明らかでしょう。
内容:
- ゲンツェンのLKシーケント計算をご存知の方への注意
- とりあえず描くぞ
- プロファイルを調べてみると
- 連言命題を構成する/連言命題を分解する基本推論
ゲンツェンのLKシーケント計算をご存知の方への注意
検索などでたまたまここに辿り着いた人が誤解するのも困るので、毎回この節を挿入することにします。
- '⇒'は含意〈条件法〉の論理結合子で、'→'がシーケントの左右を区切る記号である。
- ゲンツェンのLKシーケントでは、左辺のカンマは連言的に、右辺のカンマは選言的に解釈をする。ここでのシーケントでは、出現位置の情報を使わずに、カンマは常に連言的であり、選言的な区切り記号に縦棒'|'を使う。
- (x∈R, n∈N) のような書き方は、集合論の命題ではなくて、自由変数の型宣言(のリスト)である。自由変数の型宣言のリストをコンテキストと呼ぶ。
- 暗黙のコンテキストを使う場合もあるが、できるだけ、シーケント内に明示的にコンテキストを書き込むようにしている。
- NK/NJの証明図を推論図、LK/LJの証明図をリーズニング図と呼んで区別している。両方を同時に使うことがある。推論規則は、基本推論/基本リーズニングと呼ぶ。
- LK/LJのように、公理(基本推論)がひとつではなくて、けっこうたくさんの公理がある。その代わり、推論規則(基本リーズニング)の数を減らすようにしている。
とりあえず描くぞ
全体を一度には描けない(面積の関係で)ので、いくつかの部分に分けます。描き方は、「面積問題への対策(あるいは無策) (A21) // お約束」に従います。が、全部乗せしません。
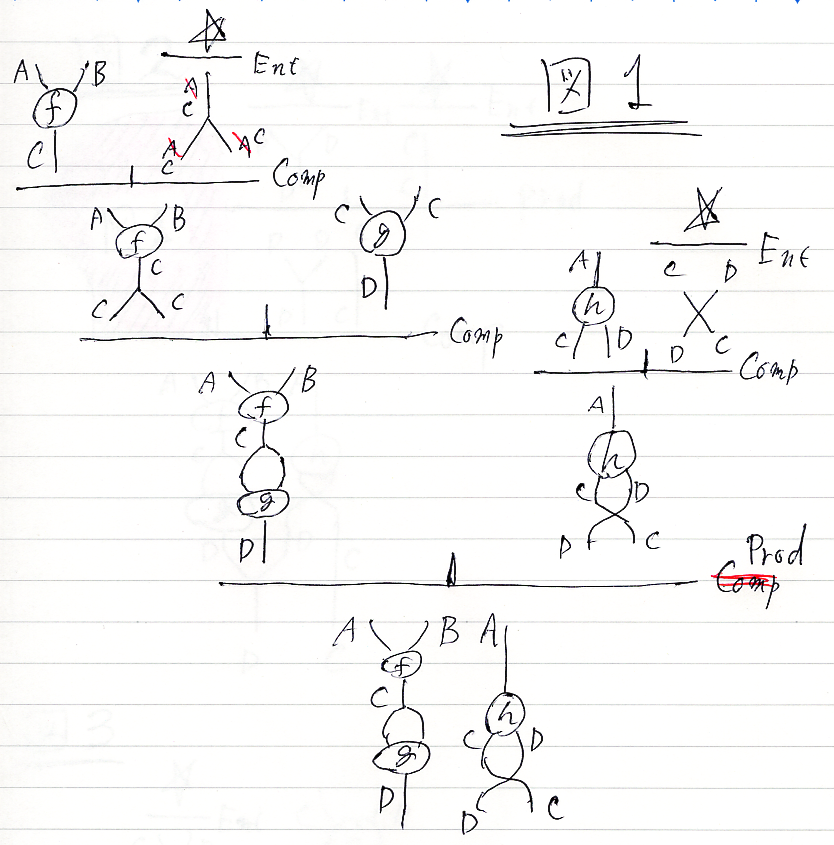
この図1を、テキストの式とプロファイルで書くと:
☆
---------- Ent
f:A,B→C dup:C→C,C ☆
---------------------- Comp ------------- Ent
f;dup:A,B→C,C g:C,C→D h:A→C,D swap:C,D→D,C
---------------------------------- Comp ------------------------ Comp
f;dup;g:A,B→D h;swap:A→D,C
------------------------------------------------ Prod
(f;dup;g)(h;swap):A,B,A→D,D,C
これも、グラフィカルな図と同じ情報を持ちます。欠点は、テキストの式だと2次元の構造が見えなくなることです。リーズニング名の代わりに演算子記号を使うのもいいかも知れません(Entは省略)。
☆
----------
f:A,B→C dup:C→C,C ☆
---------------------- ; -------------
f;dup:A,B→C,C g:C,C→D h:A→C,D swap:C,D→D,C
---------------------------------- ; ------------------------ ;
f;dup;g:A,B→D h;swap:A→D,C
------------------------------------------------
(f;dup;g)(h;swap):A,B,A→D,D,C
マイク・シュルマン〈Mike/Michael Shulman〉はこれと同じ描画法を使ってます*1。ただし、左右は逆です(その他、細かい違いはあります)。

話を戻して、図1のプロファイルだけなら:
☆
------- Ent
A,B→C C→C,C ☆
----------------- Comp ---------- Ent
A,B→C,C C,C→D A→C,D C,D→D,C
--------------------------- Comp ------------------ Comp
A,B→D A→D,C
-------------------------------------- Prod
A,B,A→D,D,C
次に、図1を一部に埋め込んだ図2。図1をはめ込む部分が目立ち過ぎだわ。斜線とピンクでキタネー。
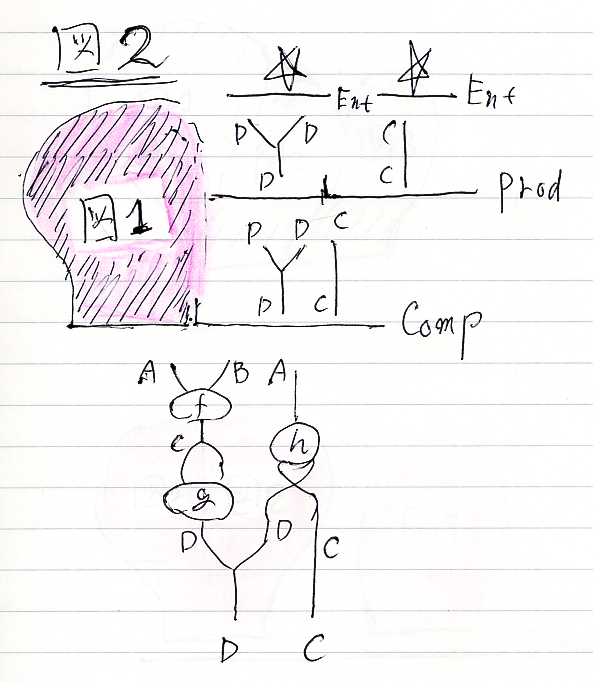
図2のプロファイルだけ:
☆ ☆
〜〜〜 ------- Ent ------ Ent
図1 D,D→D C→C
〜〜〜 ------------------ Prod
A,B,A→D,D,C D,D,C→D,C
------------------------------- Comp
A,B,A→D,Cここまでで、もとの絵の左側ができました。念の為、もとの絵を再掲。
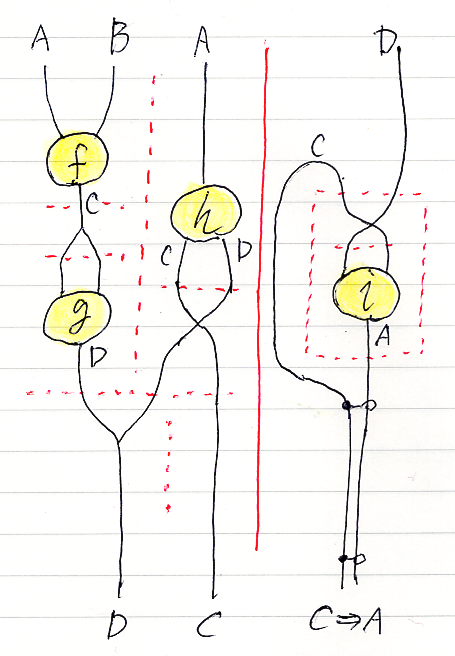
次は、右側のほうを作っていきます。アレッ、図3で、C, Dのスワップとiのラベルが間違ってる、直さん(描き直すの面倒だから)。
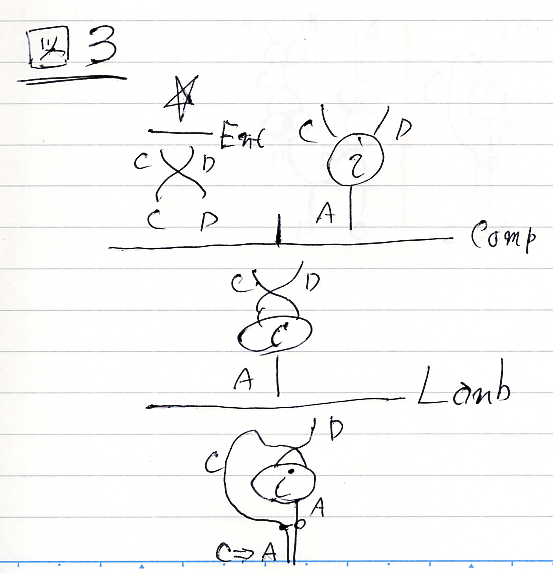
プロファイルだけなら(間違いは修正):
☆
--------- Ent
C,D→D,C D,C→A
-------------------- Comp
C,D→A
--------- Lamb
D→C⇒Aこれで、絵の左側と右側が出来たので、Sumリーズニングで選言的に併置します。あのさー、ピンクの塊が目立ち過ぎなんだけど、、、なんでこんな描き方しちゃったかなー (後悔)。
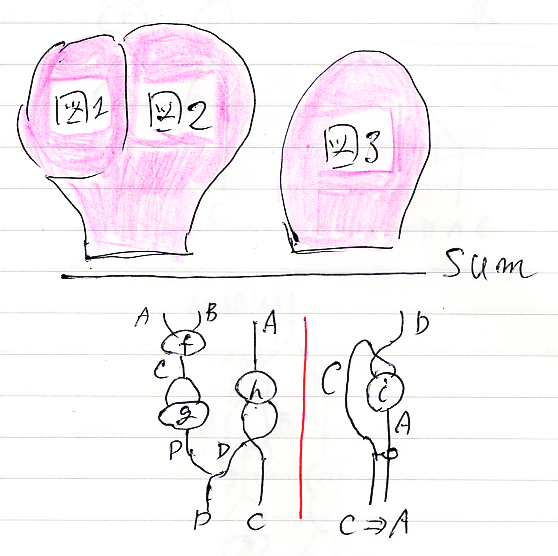
以上で、絵の構成過程であるリーズニング図が出来上がりです。注釈の区切り線や囲み線が描いてあれば、最後の絵からリーズニング図を(ほぼ)一意的に再現できます。
これは、括弧付けをきちんとした式から構文解析木が一意的に構成できることと同じです。構文解析木については「整数式の構文解析木 (A4P3)」に解説と練習問題があります。ちなみに、今回の絵の“括弧付けをきちんとした式”は:
- ( ( ((f;dupC);g)
(h;swapC,D) );(codupD
idC) )
( Λ(swapC,D;i) )
この式の構文解析木がリーズニング図なわけです。
プロファイルを調べてみると
プロファイルだけなら一枚の絵に書けるかな? できるだけ圧縮するため、Ent, Prod, Comp, Lamb を、E, P, C, L の一文字にして、空白も空けないで詰めます。
☆
------E
A,B→C C→C,C ☆
-------------C -------E
A,B→C,C C,C→D A→C,D C,D→D,C ☆ ☆ ☆
-------------------C ---------------C ------E ----E --------E
A,B→D A→D,C D,D→D C→C C,D→D,C D,C→A
-------------------------P ------------P ---------------C
A,B,A→D,D,C D,D,C→D,C C,D→A
---------------------------C -------L
A,B,A→D,C D→C⇒A
これ、最下段を書いてません。最下段まで描くと、次のようになっちゃうのです。
::: :::
::: :::
------------ ---------
A,B,A→D,C D→C⇒A
----------------------------- Sum
A,B,A | D → D,C | C⇒A最下段の推論図(=もとの推論図)のプロファイルに、カンマと縦棒の入れ子ができちゃうのです。括弧で包んでみると:
- ((A,B,A) | D) → ((D,C) | C⇒A)
こういう入れ子が、絶対にダメってわけじゃないのですが、リーズニングの計算を(極度に)複雑にしてしまうために禁止してます。もともと、推論図からリーズニング図に移行した動機が「計算が簡単になるから」*2なので、計算が複雑になる要因を許すと元も子もないのですわ。
対策として、図2のところを次の図2'のように修正します。
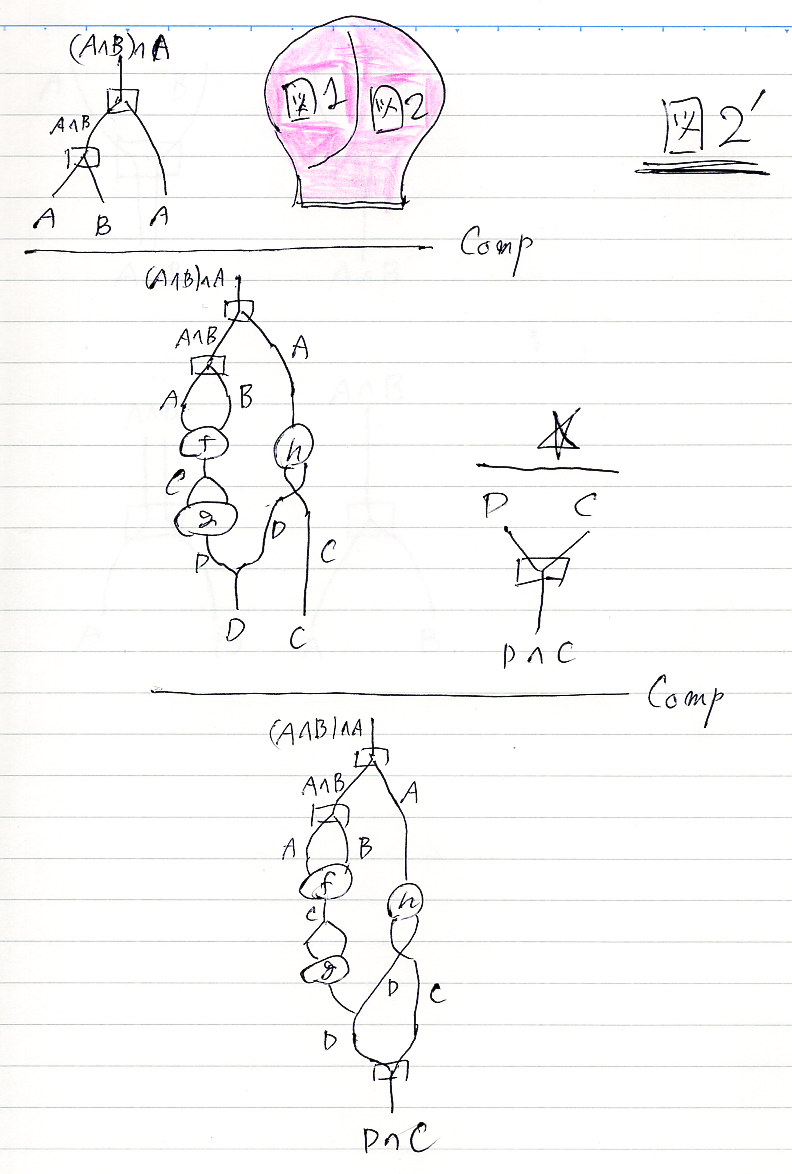
これは何をやっているのかと言うと; もとの図の左側のプロファイルが A,B,A → D,C だったのを、論理式のリストを単一論理式にしてしまうのです。
- 連言的リスト A,B,A を、単一論理式 A∧B∧C にする。
- 連言的リスト D,C を、単一論理式 D∧C にする。
- すると、A∧B∧A → D∧C というプロファイルの推論図になる。
ゲンツェンの(オリジナルの)システムだと、基本リーズニングが20個以上あり、こういうことを一発で出来る基本リーズニングも最初から備えているのだけど、基本リーズニングを6個に減らしてしまったので、次のような手順が必要です。
(A∧B)∧A→A,B,A A,B,A → D,C ☆
-------------------------------C ---------E
(A∧B)∧A→D,C D,C→D∧C
---------------------------------C
(A∧B)∧A→D∧Cこのリーズニング図(のプロファイルのみ略記)の最上段左の (A∧B)∧A→A,B,A は、基本推論ではないので、これも次のようにして作る必要があります。
☆ ☆
-----------E ----E
☆ A∧B → A, B A→A
--------------------E --------------------P
(A∧B)∧A → A∧B, A A∧B, A → A, B, A
------------------------------------------C
(A∧B)∧A → A, B, A基本リーズニングがたった6個じゃ不便だろう? って。いやっ、全然平気。マクロ・リーズニング(ユーザー定義のリーズニング)やマクロ推論(ユーザー定義の推論)をどんどん足していけば、システムの能力はいくらでも上がります。小さなコアのプログラミング言語でも、ライブラリで能力を足せるのと同じです。
僕が基本リーズニングを減らしている(代わりに基本推論がけっこう多い)のは、カリー/ハワード対応と圏論的意味論の観点を重視してるからで、趣味の問題とも言えます。
連言命題を構成する/連言命題を分解する基本推論
前節で、A, B → A∧B と A∧B → A, B というプロファイルの基本推論が出てきました。これはγ〈小文字ガンマ〉という名前で呼びたいと思います。
- γA,B:A, B → A∧B
- γA,B-1:A∧B → A, B
γA,Bとその逆であるγA,B-1は頻繁に登場するので、描画時に名前ラベルを使わないで、アイコン〈シルシモノ | マーカー〉を使います。γA,Bは、次のどちらか、
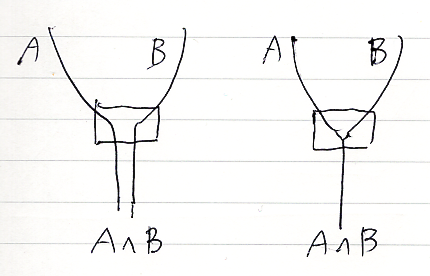
γA,B-1は次のどちらかで描くことにします。
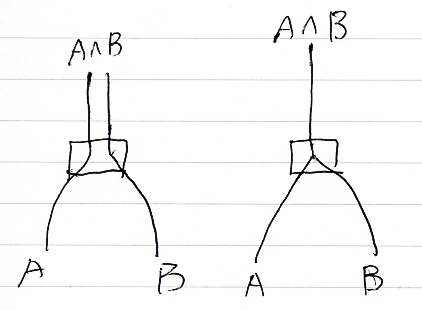
これらの推論(図)は、もちろん最初からシステムに備わる基本推論です。
*1:https://mikeshulman.github.io/catlog/catlog.pdf の p.40(ノンブル〈表示のページ番号〉は37)
*2:圏論の言葉を使うと、推論図からリーズニング図への以降は、モノイド圏の厳密化〈strictification〉をしていることです。