April 15, 2024
Semi-Simplicial Types, Part II: The Main Results
Posted by Mike Shulman
(Jointly written by Astra Kolomatskaia and Mike Shulman)
This is part two of a three part series of expository posts on our paper Displayed Type Theory and Semi-Simplicial Types. In this part, we cover the main results of the paper.
April 10, 2024
Machine Learning Jobs for Category Theorists
Posted by John Baez
Former Tesla engineer George Morgan has started a company called Symbolica to improve machine learning using category theory.
When Musk and his AI head Andrej Karpathy didn’t listen to Morgan’s worry that current techniques in deep learning couldn’t “scale to infinity and solve all problems,” Morgan left Tesla and started Symbolica. The billionaire Vinod Khosla gave him $2 million to prove that ideas from category theory could help.
Khosla later said “He delivered that, very credibly. So we said, ‘Go hire the best people in this field of category theory.’ ” He says that while he still believes in OpenAI’s continued success building large language models, he is “relatively bullish” on Morgan’s idea and that it will be a “significant contribution” to AI if it works as expected. So he’s invested $30 million more.
March 28, 2024
Why Mathematics is Boring
Posted by John Baez
I’m writing a short article with some thoughts on how to write math papers, with a provocative title. It’s due very soon, so if you have any thoughts about this draft I’d like to hear them soon!
March 23, 2024
Counting Points on Elliptic Curves (Part 3)
Posted by John Baez
In Part 1 of this little series I showed you Wikipedia’s current definition of the -function of an elliptic curve, and you were supposed to shudder in horror. In this definition the -function is a product over all primes . But what do we multiply in this product? There are 4 different cases, each with its own weird and unmotivated formula!
In Part 2 we studied the 4 cases. They correspond to 4 things that can happen when we look at our elliptic curve over the finite field : it can stay smooth, or it can become singular in 3 different ways. In each case we got a formula for number of points the resulting curve over the fields .
Now I’ll give a much better definition of the -function of an elliptic curve. Using our work from last time, I’ll show that it’s equivalent to the horrible definition on Wikipedia. And eventually I may get up the nerve to improve the Wikipedia definition. Then future generations will wonder what I was complaining about.
March 13, 2024
Counting Points on Elliptic Curves (Part 2)
Posted by John Baez
Last time I explained three ways that good curves can go bad. We start with an equation like
where is a cubic with integer coefficients. This may define a perfectly nice smooth curve over the complex numbers — called an ‘elliptic curve’ — and yet when we look at its solutions in finite fields, the resulting curves over those finite fields may fail to be smooth. And they can do it in three ways.
Let’s look at examples.
March 10, 2024
Counting Points on Elliptic Curves (Part 1)
Posted by John Baez
You’ve probably heard that there are a lot of deep conjectures about -functions. For example, there’s the Langlands program. And I guess the Riemann Hypothesis counts too, because the Riemann zeta function is the grand-daddy of all -functions. But there’s also a million-dollar prize for proving the Birch-Swinnerton–Dyer conjecture about -functions of elliptic curves. So if you want to learn about this stuff, you may try to learn the definition of an -function of an elliptic curve.
But in many expository accounts you’ll meet a big roadblock to understanding.
The -function of elliptic curve is often written as a product over primes. For most primes the factor in this product looks pretty unpleasant… but worse, for a certain finite set of ‘bad’ primes the factor looks completely different, in one of 3 different ways. Many authors don’t explain why the -function has this complicated appearance. Others say that tweaks must be made for bad primes to make sure the -function is a modular form, and leave it at that.
I don’t think it needs to be this way.
March 9, 2024
Semi-Simplicial Types, Part I: Motivation and History
Posted by Mike Shulman
(Jointly written by Astra Kolomatskaia and Mike Shulman)
This is part one of a three-part series of expository posts on our paper Displayed Type Theory and Semi-Simplicial Types. In this part, we motivate the problem of constructing SSTs and recap its history.
March 3, 2024
Modular Curves and Monstrous Moonshine
Posted by John Baez
Recently James Dolan and I have been playing around with modular curves — more specifically the curves and , which I’ll explain below. Monstrous Moonshine says that when is prime, the curve has genus zero iff divides the order of the Monster group, namely
Just for fun we’ve been looking at , among other cases. We used dessins d’enfant to draw a picture of , which seems to have genus , so for to have genus zero it seems we want the picture for to have a visible two-fold symmetry. After all, the torus is a two-fold branched cover of the sphere, as shown by Greg Egan here:
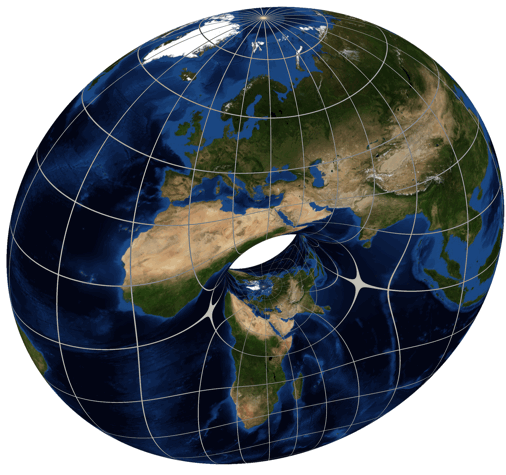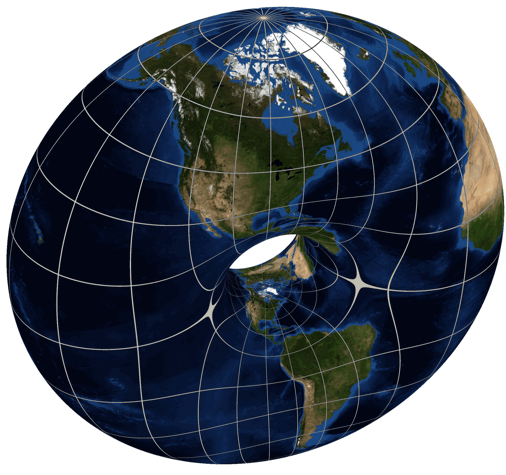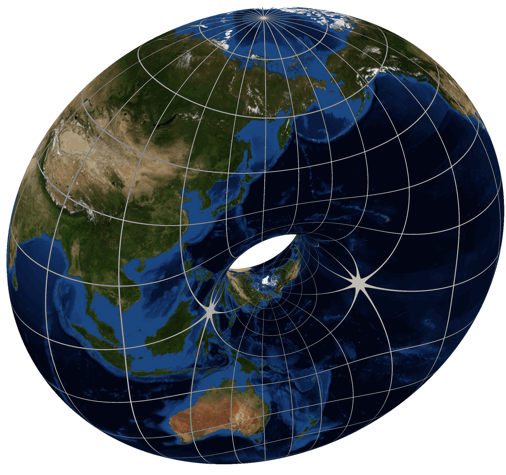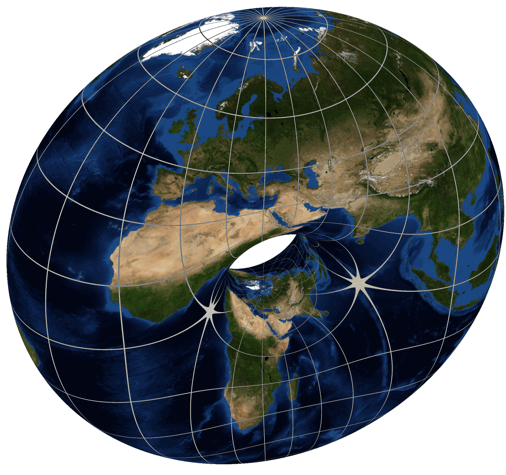
But we’re not seeing that two-fold symmetry. So maybe we’re making some mistake!
Maybe you can help us, or maybe you’d just like a quick explanation of what we’re messing around with.
February 20, 2024
Spans and the Categorified Heisenberg Algebra
Posted by John Baez
I’m giving this talk at the category theory seminar at U. C. Riverside, as a kind of followup to one by Peter Samuelson on the same subject. My talk will not be recorded, but here are the slides:
Abstract. Heisenberg reinvented matrices while discovering quantum mechanics, and the algebra generated by annihilation and creation operators obeying the canonical commutation relations was named after him. It turns out that matrices arise naturally from ‘spans’, where a span between two objects is just a third object with maps to both those two. In terms of spans, the canonical commutation relations have a simple combinatorial interpretation. More recently, Khovanov introduced a ‘categorified’ Heisenberg algebra, where the canonical commutation relations hold only up to isomorphism, and these isomorphisms obey new relations of their own. The meaning of these new relations was initially rather mysterious, at least to me. However, Jeffery Morton and Jamie Vicary have shown that these, too, have a nice interpretation in terms of spans.
February 14, 2024
Cartesian versus Symmetric Monoidal
Posted by John Baez
James Dolan and Chris Grossack and I had a fun conversation on Monday. We came up some ideas loosely connected to things Chris and Todd Trimble have been working on… but also connected to the difference between classical and quantum information.
February 4, 2024
The Atom of Kirnberger
Posted by John Baez
The 12th root of 2 times the 7th root of 5 is
And since the numbers 5, 7, and 12 show up in scales, this weird fact has implications for music! It leads to a remarkable meta-meta-glitch in tuning systems. Let’s check it out.
January 29, 2024
Axioms for the Category of Finite-Dimensional Hilbert Spaces and Linear Contractions
Posted by Tom Leinster
Guest post by Matthew di Meglio
Recently, my PhD supervisor Chris Heunen and I uploaded a preprint to arXiv giving an axiomatic characterisation of the category of finite-dimensional Hilbert spaces and linear contractions. I thought it might be nice to explain here in a less formal setting the story of how this article came to be, including some of the motivation, ideas, and challenges.
January 24, 2024
Summer Research at the Topos Institute
Posted by John Baez
Are you a student wanting to get paid to work on category theory in Berkeley? Then you’ve got just one week left to apply! The application deadline for Research Associate positions at the Topos Institute is February 1st.
Details and instructions on how to apply are here:
December 4, 2023
Magnitude 2023
Posted by Tom Leinster
I’m going to do something old school and live-blog a conference: Magnitude 2023, happening right now in Osaka. This is a successor to Magnitude 2019 in Edinburgh and covers all aspects of magnitude and magnitude homology, as well as hosting some talks on subjects that aren’t magnitude but feel intriguingly magnitude-adjacent.
Slides for the talks are being uploaded here.
What is magnitude? The magnitude of an enriched category is the canonical measure of its size. For instance, the magnitude of a set (as a discrete category) is its cardinality, and the magnitude of an ordinary category is the Euler characteristic of its nerve. For metric spaces, magnitude is something new, but there is a sense in which you can recover from it classical measures of size like volume, surface area and dimension.
What is magnitude homology? It’s the canonical homology theory for enriched categories. The magnitude homology of an ordinary category is the homology of its classifying space. For metric spaces, it’s something new, and has a lot to say about the existence, uniqueness and multiplicity of geodesics.
Let’s go!
December 1, 2023
Adjoint School 2024
Posted by John Baez
Are you interested in applying category-theoretic methods to problems outside of pure mathematics? Apply to the Adjoint School!
Apply here. And do it soon.
December 31, 2023. Application Due.
February - May, 2024. Learning Seminar.
June 10 - 14, 2024. In-person Research Week at the University of Oxford, UK.
 Posts with this logo use
Posts with this logo use 















